Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 111
O cabo tem uma massa por unidade de comprimento de . Determine o comprimento total mais curto do cabo que pode ser suspenso em equilibro.
Passo 1
O problema quer que a gente encontre o comprimento total mais curto do cabo que pode ser suspenso em equilibro.
Vamos começar fazendo um diagrama de corpo livre, assim:
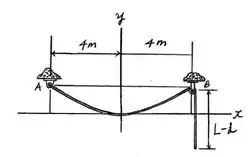
Onde o carregamento pode ser descrito como:
Percebeu aí que o problema não deu o peso por unidade de comprimento e sim a massa, por isso eu multipliquei pela gravidade, cuidado com isso, as vezes aparece.
Passo 2
Nós notamos que na figura do problema, é o ponto mais baixo do cabo, vamos pegar a segunda derivada da equação do cabo, logo:
Se nós consideramos , então , logo:
E integrando isso:
Vamos encontrar , pra isso a gente usa a condição inicial, de que na origem, e então:
Logo é igual a .
Ficamos com:
Agora, vamos dar uma ajeitada e tentar simplicar isso, calma, eu sei que parece muito estranho:
Agora lembra que , aí ficamos com:
Passo 3
Vamos agora pegar o diagrama do corpo livre, assim:
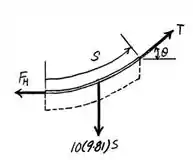
E usamos as equações de equilíbrio nos dois eixos:
Eliminando , temos:
Então igualamos a equação derivada:
Assim encontramos:
O comprimento do cabo entre e e dado por:
Então, o comprimento do cabo pendurado é:
A tração do cabo em é igual ao peso do cabo que está pedurado, concorda comigo? Então, fica:
Agora, calculamos o ângulo que o cabo faz em relação a horizontal em :
Agora, calculamos o ângulo:
Logo:
Passo 4
Combinando as equações:
A gente encontra que:
Sabendo que , a gente pode escrever:
Passo 5
Então agora, derivamos o comprimento em relação a , é mais simples do que parece:
Resolendo por tentativa e erro, encontramos:
Por ultimo substituímos na equação que já tínhamos encontrado para o comprimento, lembra?
Assim, temos como resposta: