Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas fundamentais - Ex. 8
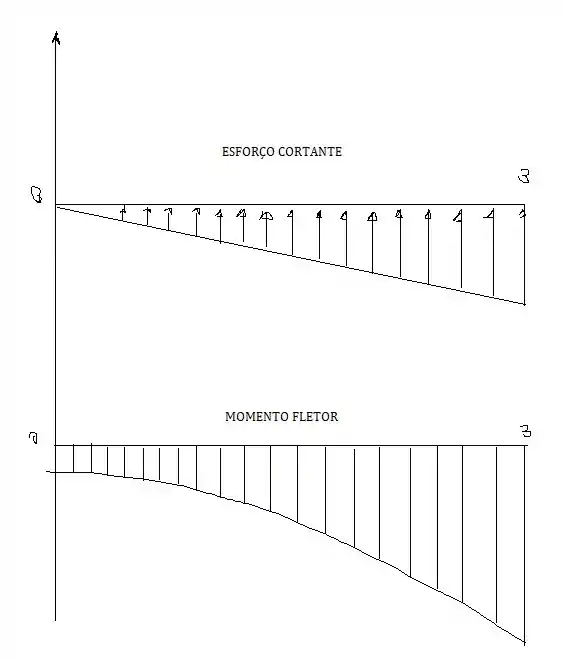
Determine o esforço cortante e o momento fletor como uma função de , e depois construa os diagramas de esforço cortante e de momento fletor.
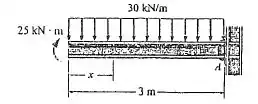
Passo 1
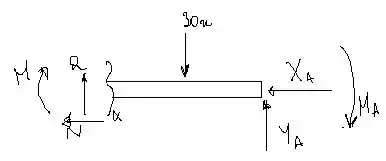
Vamos desenhar o diagrama de corpo livre da viga, beleza?
Vamos concentrar essa carga distribuída em um ponto com a finalidade de descobrirmos os valores das reações de apoio dessa viga. Assim,
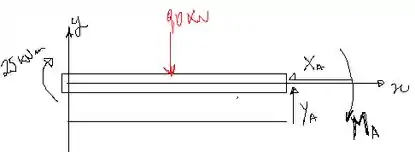
Passo 2
Vamos agora olhar para a porção que compreende o intervalor .
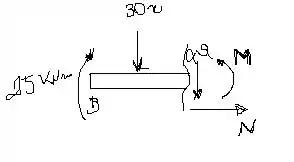
De para :
Passo 3
De para :
Resposta
Exercícios de Livros Relacionados
141- Desenvolva expressões para o cortante V e o momento fletor M em função de x para a viga em balanço do Prob. 5/108 novamente mostrada aqui.
142- A viga em balanço curva tem a forma de um quarto de círculo. Determine as expressões para o cortante V e o momento fletro M em função de θ .
140- Desenvolva expressões para o cortante V e o momento fletor M em função de x para a viga em balanço carregada como mostrado.
Determine a força normal, o esforço cortante e o momento no ponto C .
Determine a força normal, o esforço cortante e o momento no ponto C .