Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 17
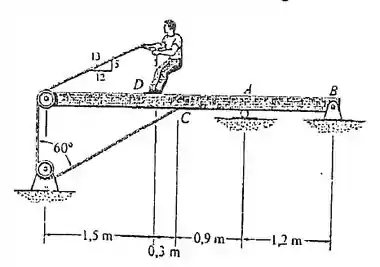
O menino de está sobre a viga e puxa a corda com uma força de . Se , determine a força de atrito entre seus sapatos e a viga e as reações em e . A viga é uniforme e tem um peso de . Despreze a dimensão das polias e a espessura da viga.
Passo 1
Falaaa, querido!
O problema pede que encontremos a força de atrito entre os sapatos do menino e a viga, e as reações em e .
Vamos começar analisando o menino. Olha um DCL (vamos simplificar o menino por um retângulo, tá?):
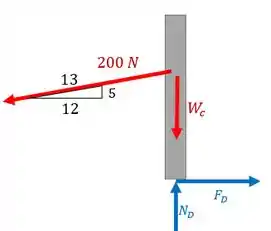
Ele tende a deslizar para a esquerda, por isso a força de atrito está para direita. Como ele puxa a corda, a reação da corda é puxá-lo, por isso o sentido da força de . E não podemos esquecer da força normal e o peso do menino.
Usando as equações de equilíbrio:
Agora, no eixo :
Passo 2
Precisamos avaliar se o menino desliza ou não, para ver se realmente estamos em equilíbrio.
Se a gente considerar que ele está quase deslizando, temos
E aplicamos o coeficiente de atrito dado e a normal achada:
O menino não deslizou porque o atrito real foi menor do que o atrito para o caso de deslizamento .
Passo 3
Vamos olhar a viga agora. Lembrando que a força na corda é a mesma, igual a , em todos os pontos, e os esforços nela são transmitidos para a viga também através de roldanas. Colocamos na viga também as reações a presença do menino. Um DCL:
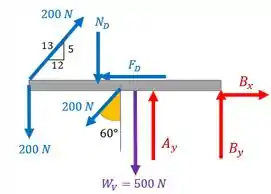
Lembrando que a gente precisa considerar o peso da viga. Tem muita forcinha aí né? Calma, respira fundo. A gente vai fazendo com cuidado e no final dá certo.
Agora, usando a equação de equilíbrio para o momento em , adotando o sentido anti-horário como positivo. As componentes horizontais das forças e as forças horizontais não vão gerar momento. Então foco nas componentes e forças verticais aqui:
Assim encontramos:
Passo 4
Agora, as forças que estão agindo na viga. Pelo somatório na horizontal:
E fazendo o mesmo no eixo encontraremos:
Esse sinal de menos só representa que ela está no sentido inverso ao que aparece no DCL.
Prontinho! Ufa! Terminamos e arrasamos!