Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 119
O cabo de vão e uma viga simplesmente apoiada de mesmo vão estão sujeitos a carregamentos verticais idênticos, como mostra a figura. Mostre que a intensidade do momento fletor no ponto da viga é igual ao produto , sendo a intensidade do componente horizontal da força de tração no cabo e a distância vertical entre o ponto e a corda que une os pontos de apoio e .
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar pra gente:
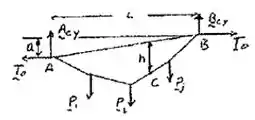
E analisando a o momento total sabendo que o corpo encontrasse em equilíbrio, a gente encontra:
Passo 2
Show de bola, agora vamos analisar o cabo :
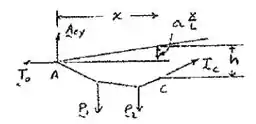
Então, podemos descrever os momentos do cabo entre e , para isso faremos:
Passo 3
Agora, vamos analisar o vão:
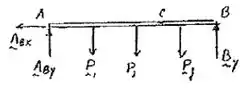
Vamos analisar o momento, utilizando como eixo de rotação:
E usando como o eixo de rotação:
Passo 4
Por fim, a gente usa apenas a parte do vão:
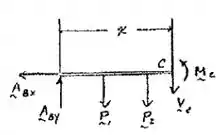
Onde podemos escrever apenas nessa parte como:
Substituindo o que já tínhamos encontrado e simplificando ao máximo, a gente chega em: