Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 135

Um fio de 90   m de comprimento está suspenso por dois pontos de igual elevação, que estão afastados 60   m entre si. Sabendo que a tração máxima é 300   N , determine (a) a flecha do fio e (b) a massa total do fio.

Passo 1

Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:

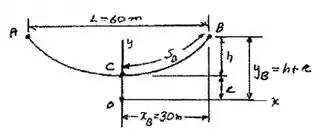
Com isso, de cara a gente já tem alguns valores:

s B = 45   m

x B = 60 2 = 30   m

Passo 2

Show de bola, agora a gente pode usar a equação 7.15 :

s B = c sinh ⁡ x B c

→ 45 = c sinh ⁡ 30 c

Resolvendo essa equação, encontramos:

c = 18,494   m

Passo 3

Calma, tá quase acabando. Vamos usar a equação 7.16 :

y B = c cosh ⁡ x B c

→ y B = 18,4941 sinh ⁡ 30 18,4941

→ y B = 48,652   m

Passo 4

Por fim, a gente pode achar h B :

h B = y B - c

→ h B = 48,652 - 18,494

→ h B = 30,158   m

E usando a equação 7.18 para encontrarmos w :

T = w y B

→ 300 = w 48,652

→ w = 6,166   N / m

E como isso a gente encontra o peso do cabo:

P = 6,166 ⋅ 90 = 554,96   N

Com o peso a gente encontra a massa fácinho:

P = m g

→ 554,96 = m ⋅ 9,81

→ m = 56,57   k g

Resposta

h B = 30,158   m

m = 56,57   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localização do máximo valor absoluto do momento fletor.
Para a viga e o carreamento mostrados nas figuras, a Trace os diagramas de esforço cortante e de momento fletor, b determine os valores absolutos máximos do esforço cortante e do momento fletor..
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localizaão do momento fletor máximo.
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localizaão do momento fletor máximo.
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localização do máximo valor absoluto do momento fletor.