Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 158
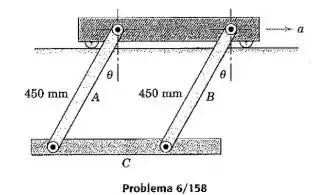
Cada uma das barras e tem uma massa de e a barra tem uma massa de . calcule o angulo assumido pelas barras se o corpo a que estão fixadas recebe uma aceleração horizontal constante de .
Passo 1
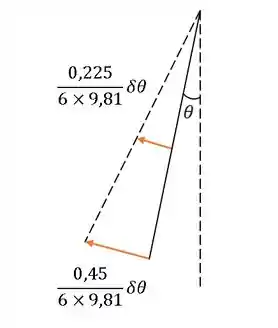
A figura ilustra o deslocamento virtual que cada barra assume.
Assumindo na altura do corpo que possui aceleração horizontal conhecida , temos que a energia gravitacional do sistema é dada por
Simplificando, obtemos
Assim, o trabalho virtual fica
Passo 2
A variação diferencial na energia cinética equivale ao trabalho diferencial realizado sobre o sistema pelas forças reultantes. Assim, para a energia cinética, temos
Simplificando, encontramos
Passo 3
Por fim, sabemos que
Substituindo as expressões encontradas para e , ficamos com
Resolvendo para , achamos
Resposta
Exercícios de Livros Relacionados
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros. Se ele é solto do repouso no topo da estrutura A, determine a altura mínima h da estrutura de maneira que o carrinho dê a
O anel de 2,5 kg é solto do repouso em A e desloca-se ao longo da guia sem atrito. Determine a velocidade do anel quando ele bate no apoio B. A mola tem um comprimento não deformado de 0,15m.
O anel de 2kg é submetido a uma velocidade para baixo de 4m/s quando está em A. Se a mola tem um comprimento não deformado de 1m e uma rigidez k=30N/m, determina a velocidade do anel em s=1m
O anel C de 4kg tem uma velocidade v A = 2 m/s quando está em A. Se a barra-guia é lisa, determine a velocidade do anel quando ele está em B. A mola tem um comprimento não deformado l a = 0,2 m.
O bloco de 375 N (massa =37,5 kg) é solto do repouso 1,5 m acima da placa. Determine a compressão de cada mola quando o bloco instantaneamente chega ao repouso após bater na placa. Despreze a massa da