Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 28

Cada uma das duas barras tem uma massa m e um comprimento l, e repousam sobre o plano horizontal liso. Se um impulso I é aplicado em um ângulo de 45° com uma das barras no meio do comprimento, como mostrado, determine a velocidade angular de cada barra logo após o impacto. As barras estão conectadas por pinos em B.

Passo 1

Para resolver esse exercício, iremos separar o conjunto e aplicar o princípio do impulso e momento para a barra BC e depois para a barra AB. Para auxiliar, segue esquema representativo das barras BC e AB, respectivamente, para aplicação do princípio do impulso e momento:

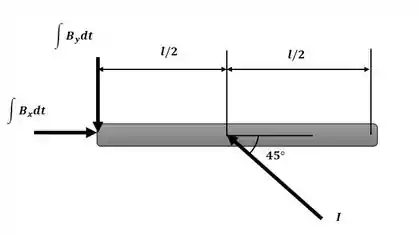
Sendo assim, para a barra BC

↺ +   H G 1 + ∑ ∫ t 1 t 2 M G d t = H G 2

0 + ∫ B y d t l 2 = I G ω B C

Essa será nossa equação número 1. Agora aplicaremos o princípio do impulso e momento na direção y:

+ ↑   m v G y 1 + ∑ ∫ t 1 t 2 F y d t = m v G y 2

0 - ∫ B y d t + I s e n 45 ° = m v G y

Essa será nossa equação número 2.

Passo 2

Agora podemos aplicar o princípio do impulso e momento angular para a barra AB:

↺ +   H G 1 + ∑ ∫ t 1 t 2 M G d t = H G 2

0 + ∫ B y d t l 2 = I G ω A B

Essa será nossa equação número 3. Agora aplicaremos o princìpio do impulso e momento linear na direção y:

+ ↑   m v G y 1 + ∑ ∫ t 1 t 2 F y d t = m v G y 2

0 + ∫ B y d t = m v G ' y

Essa será nossa equação número 4. Podemos ainda escrever a velocidade do ponto B com o auxílio das seguintes imagens das barras BC e AB, respectivamente:

v B = v G ' + v B / G ' = v G + v B / G

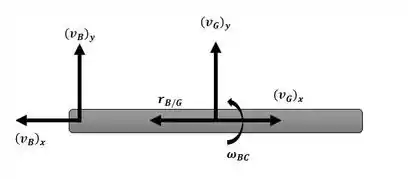
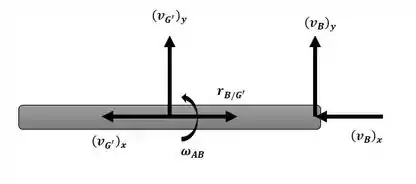
Na direção y, a equação se torna:

v B y = v G ' y + ω A B l 2 = v G y - ω B C l 2

Essa será nossa equação número 5.

Passo 3

Agora, iremos igualar as equações 1 e 2 pelo termo integral, sendo assim:

I G ω B C 2 l = I s e n 45 ° - m v G y

Seguindo o mesmo procedimento para as equações 3 e 4:

I G ω A B 2 l = m v G ' y

E igualando as equações 1 e 3 pelo termo integral, podemos encontrar a relação entre as duas velocidades angulares:

I G ω B C = I G ω A B

ω B C = ω A B

Agora, substituindo essas relações na equação 5:

1 m 2 l I G ω A B + ω A B l 2 = - I G ω A B m 2 l + I m s e n 45 ° - ω A B l 2

4 m l I G ω A B + ω A B l = I m s e n 45 °

4 m l 1 12 m l 2 ω A B + ω A B l = I m s e n 45 °

4 3 ω A B l = I m s e n 45 °

ω A B = ω B C = 3 4 2 I m l

Resposta

ω A B = ω B C = 3 4 2 I m l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pequena esferaBde massamé presa em uma corda inextensível de comprimento 2a, que passa em torno da cavilhaAe é presa no suporte fixoO. A esfera é mantida próxima ao suporteOe liberada com velocida
Um martelo de 650 kg de um bate-estaca cai de uma altura de 1,2 m sobre o topo de uma estaca de construção de 140 kg, movendo-se 110 mm no chão. Considerando um impacto plástico perfeito (e= 0), deter
Um ônibus espacial está indo de encontro a uma estação espacial que está em órbita circular a uma altitude de 400 km acima da Terra. O ônibus deve alcançar uma altitude de 60 km, quando seus motores s
Uma pequena esferaApresa a uma cordaACé liberada do repouso na posição mostrada na figura e atinge uma esfera idênticaBsuspensa pela corda verticalBD. Se o máximo ângulo θ B formado pela cordaBDcom a
Um blocoAde 2 kg é empurrado contra uma mola comprimindo a na distânciax= 0,1 m. O bloco é então liberado do repouso e desliza num declive de 20° até atingir uma esferaBde 1 kg que está suspensa por u