Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 21

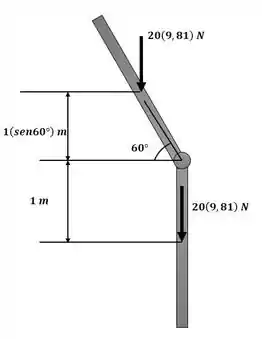
Por razões de segurança, a perna do apoio de 20 kg de um sinal é projetada para quebrar com uma resistência desprezível em B quando a perna é submetida ao impacto de um carro. Supondo que a perna está presa com um pino em A e aproxima-se de uma barra fina, determine o impulso que o para-choque do carro exerce sobre ela, se após o impacto a perna parecer girar no sentido horário para um ângulo máximo θ m á x = 150 ° .

Passo 1

Para esse exercício, consideraremos a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício calculando o momento de inércia da perna de apoio em torno do ponto A:

I A = 1 3 20 2 2

I A = 26,667   k g . m 2

Passo 2

Agora podemos aplicar o princípio do impulso e da quantidade de movimento angular para a perna de apoio em torno do ponto A com o auxílio do esquema a seguir:

↺ +   I A ω 1 + ∑ ∫ t 1 t 2 M A d t = I A ω 2

0 + I 1,75 = 26,667 ω 2

ω 2 = 0,065625 I

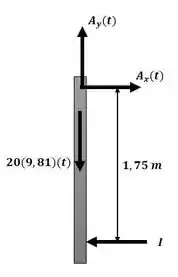
Passo 3

Agora podemos aplicar a equação da conservação da enegia mecânica apresentada no capítulo 18 com o auxílio da imagem a seguir que compara o estado inicial e final da perna:

T 2 + V 2 = T 3 + V 3

1 2 26,667 0,065625 I 2 + 20 9,81 - 1 = 0 + 20 9,81 1 s e n 60 °

I = 79,8   N . s

Resposta

I = 79,8   N . s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos A e B têm massa de 0,5 kg cada, e o bloco C de 1,5 kg. O coeficiente de atrito entre os blocos e o plano é k =0,30. Inicialmente, o bloco A move-se a uma velocidade vo= 4 m/s e os blocos B e
Uma bolaBde 70 g é largada de uma alturah0= 1,5 m e alcança uma alturah2= 0,25 m após dois quiques em placas idênticas de 210 g.AplacaArepousa diretamente no chão duro, ao passo que a placaCrepousa so
Quando a corda está a um ângulo de α=30 ° , a esferaAde 0,5 kg tem uma velocidadev0= 1,2 m/s. O coeficiente de restituição entreAe cunhaBde 0,9 kg é 0,7 e o comprimento da cordal= 0,8 m. A constante d
O raio da órbita da lua de um determinado planeta é igual a duas vezes o raio desse planeta. Denotando por p a densidade média do planeta, mostra que o tempo necessário para a lua completar uma revolu
Para a partícula do Problema 12.74, determine o componente tangencial Ft da força central F ao longo da tangente ao caminho da partícula para (a) θ = 0, (b) θ - 45 °.