Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 26

O corpo e a caçamba de uma minicarregadeira têm uma massa de 1000 kg, e seu centro de gravidade está localizado em G. Cada uma das quatro rodas têm uma massa de 50 kg e um raio de giração em relação a seu centro de gravidade de 0,3 m. Se o motor fornece um torque M = 150 N.m para cada uma das rodas motrizes traseiras, determine a velocidade da minicarregadeira em t = 10 s, partindo do repouso. As rodas rolam sem deslizar.

Passo 1

Para resolver esse exercício, adotaremos a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício calculando o momento de inércia dos pares de rodas com relação a seus centros de massa:

I R = 2 m k 2 = 2 50 0,3 2

I R = 9   k g . m 2

Como as 4 rodas rolam sem deslizar, podemos relacionar suas velocidades linear e angular da seguinte forma:

ω = v r = v 0,375 → ω = 2,667 v

Passo 2

Agora podemos aplicar o princípio do impulso e momento angular nos pontos de contato com o chão C (traseira) e D (dianteira), sendo assim, para a roda traseira:

↺ +   H C 1 + ∑ ∫ t 1 t 2 M C d t = H C 2

0 + 2 50 10 - A x 10 0,375 = 9 2,667 v + 2 50 v ( 0,375 )

A x = 266,67 - 16,4 v

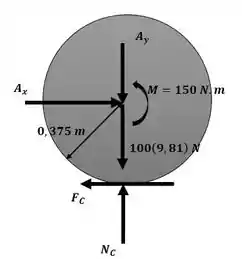
Essa será nossa equação número 1. Agora para o ponto de contato na roda dianteira em D:

↻ +   H D 1 + ∑ ∫ t 1 t 2 M D d t = H D 2

0 + B x 10 0,375 = 9 2,667 v + 2 50 v 0,375

B x = 16,4 v

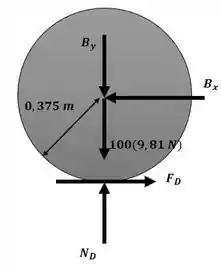
Essa será nossa equação número 2

Passo 3

Agora aplicaremos o princípio do impulso e do momento linear na direção x com o auxílio do esquema do corpo da minicarregadeira a seguir:

+ ←   m v G x 1 + ∑ ∫ t 1 t 2 F x d t = m v G x 2

0 + A x 10 - B x 10 = 1000 v

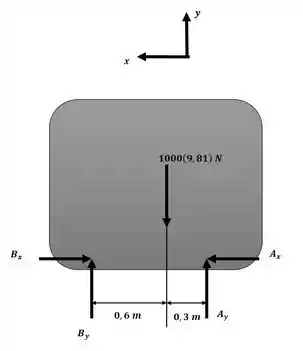
Essa será nossa equação número 3. Agora já conseguimos resolver o sistema de equações encontrado no passo 2. Isolaremos A x da equação 1 e B x da equação 2 e substituir esses valores na equação 3:

0 + A x 10 - B x 10 = 1000 v

266,67 - 16,4 v 10 - 16,4 v 10 = 1000 v

v = 2,01   m / s

Resposta

v = 2,01   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de massa m é projetada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se move sob uma força central F direcionada para longe do centro de força O. Sabendo que a part
Mostre que o raio r da órbita de uma lua de um determinado planeta pode ser determinado a partir dos raios R do planeta, da aceleração da gravidade na superfície do planeta e do tempo necessário para
Para a partícula do Problema 12.76 mostre (a) que a velocidade da partícula e a força central F são proporcionais à distância r da partícula ao centro de força O, (b) que o raio de curvatura do caminh
Uma espaçonave é colocada em uma órbita polar em torno do planeta Marte a uma altitude de 380 km. Sabendo que a densidade média de Marte é 3,94 Mg / m³ e que o raio de Marte é 3397 Km, determine (a) o
Uma espaçonave de 600 kg é colocada primeiramente em uma órbita circular em torno da Terra a uma altitude de 4.500 km e, então, transferida para uma órbita circular em torno da Lua. Sabendo que a mass