Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 201

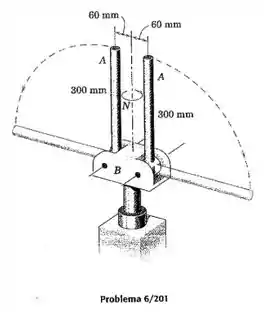
Cada uma das duas barras uniformes A de 300   m m possui uma massa de 1,5   k g e é articulada em sua extremidade à base B que está girando. A base com 4   k g tem um raio de giração de 40   m m e está inicialmente girando livremente em torno de seu eixo vertical com uma velocidade de 300   r p m e com as barras travadas nas posições verticais. Se as travas são liberadas e as barras assumem as posições horizontais, calcule a nova velocidade de rotação N do conjunto.

Passo 1

Pela conservação da quantidade de movimento angular, temos

H 1 = H 2

Inicialmente, temos

H 1 b a r r a = 2 I ω = 2 × 1,5 0,06 2 300 × 2 π 60 = 0,339   k g × m 2 / s

H 1 b a s e = M k 2 ω = 4 0,04 2 300 × 2 π 60 = 0,201   k g × m 2 / s

Na configuração em que as barras assumem as posições horizontais, temos

H 2 b a r r a = 2 × I - + m d 2 ω = 2 1 12 1,5 0,3 2 + 0,15 1,5 + 0,06 2 × 2 π N 60

Simplificando a equação anterior, ficamos com

H 2 b a r r a = 0,01621 N

Para a base, temos

H 2 b a s e = M k 2 N = 4 0,04 2 N × 2 π 60 = 0,00067 N

Passo 2

Retomando a equação da conservação da quantidade de movimento angular:

H 1 = H 2

Substituindo os valores encontrados,

0,339 + 0,201 = 0,01621 N + 0,00067 N

Por fim, resolvendo para N , achamos

N = 32   r p m

Resposta

N = 32   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A esfera de 500g está se deslocando no plano horizontal x - y com uma velocidaed de 3m / s na direção mostrada e encontra um fluxo constante de ar na direção x . Se o fluxo de ar exerce uma força esse
Uma jogadora de tênis rebate a bola de tênis com sua raquete enquanto a bola ainda está subindo. A velocidade da bola antes do impacto com a raquete é v 1 = 15m / s e após o impacto sua velocidade é v
O tampão cilíndrico A de massa m A é liberado a partir do repouso em B e desliza para baixo na guia circular lisa. O tampão atinge o bloco C e se encaixa nele. Escreva a expressão para a distância s q
Os dois vagões de mina de massas iguais são conectados por uma corda que está inicialmente frouxa. O vagão A recebe um empurrão que transmite a ele uma velocidade de 1,2m / s com o vagão B inicialment
A bola de beisebol está se deslocando com uma velocidade horizontal de 135 k m / h pouco antes do impacto com o bastão. Logo após o impacto, a velocidade da bola de 146g é de 210k m / h direcionada a