Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 214

O bloco retangular uniforme com as dimensões fornecidas é deixado cair do repouso a partir da posição mostrada. A extremidade A atinge a borda em B e se prende a ela. Determine a velocidade angular ω do bloco imediatamente após se fixar em B. encontre também a porcentagem n da perda de energia durante a fixação da extremidade para o caso em que b = c .

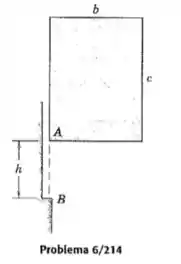
Passo 1

Como estamos calculando a velocidade angular imediatamente após o bloco se prender a B, a quantidade de movimento angular em relação a B será zero:

∆ H B = 0

Logo:

I A ω - m v b 2 = 0

A primeira parte da equação corresponde à rotação em relação ao ponto A, e a segunda à translação do centro de massa.

Passo 2

Como o bloco chega em queda livre no ponto B, pela conservação de energia:

1 2 m v 2 = m g h

v = g h

E agora calculando o momento de inercia em relação ao eixo que passa no ponto A:

I A = 1 12 m b 2 + c 2 + m b 2 2 + c 2 2 = 1 3 m b 2 + c 2

Passo 3

Substituindo o que encontramos na equação do Passo 1:

1 3 m b 2 + c 2 ω - m g h b 2 = 0

Isolando ω :

ω = 3 b g h 2 b 2 + c 2

Passo 4

E para calcularmos a porcentagem de perda de energia, faremos a seguinte razão:

n = ∆ E E = 1 2 m v 2 - 1 2 I A ω 2 1 2 m v 2

Que será a diferença entre a energia cinética de translação do bloco e a energia cinética de rotação devido à fixação na extremidade. E a razão será para calcular em porcentagem.

Passo 5

Como para esse caso, b = c :

n = 1 - 1 3 m 2 c 2 3 c g h 2 2 c 2 2 m g h 2

Simplificando:

n = 1 - 3 8 = 5 8 = 62.5 %

Resposta

ω = 3 b g h 2 b 2 + c 2

n = 62.5 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das quatro esferas de massa m é tratada como uma partícula. As esferas A e B são montadas em uma haste leve e estão inicialmente girando com uma velocidade angular ω 0 em tordo de um eixo ver
O pêndulo simples de massa m e comprimento l é liberado a partir do repouso em θ = 0 . Utilizando apenas o principio do impulso angular e quantidade de movimento, determine a expressão para θ ¨ em ter
Uma pequena partícula de 0,1k g recebe uma velocidade de 2 m / s sobre o plano horizontal x - y e é guiada pela barra curva fixa. O atrito é desprezível. Quando a partícula cruza o eixo y em A , sua v
Um pêndulo consiste em duas massas concentradas de 3,2k g posicionadas como mostrado em uma barra leve, porém rígida. O pêndulo está oscilando pela posição vertical com uma velocidade angular no senti
No ponto A de maior aproximação com o Sol, um cometa tem uma velocidade v A = 57,45 10 3 m / s . Determine as componentes radial e transversal de sua velocidade v B no ponto B, onde a distância radial