Quatro hastes esbeltas idênticas, cada uma de massa m, são soldadas em suas extremidades para formar um quadrado, e os vértices são em seguida soldados a um aro leve de metal com raio . Se o conjunto rígido das hastes e do aro rola para baixo na inclinação, determine o valor mínimo do coeficiente de atrito estático que impedirá o deslizamento.
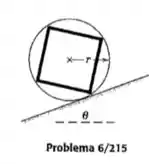
Passo 1
Precisaremos encontrar primeiro o momento de inercia do sistema, para encontrarmos o momento total em relação ao centro de massa do corpo, como o corpo giram em torno do centro da circunferência, o momento de inércia será:
O raio da circunferência é r, então a distância do centro até o vértice do quadrado será r, e portando, cada barra terá comprimento:
Por isso o momento de inércia é escrito dessa maneira.
Passo 2
Agora precisaremos calcular o momento em relação ao centro de massa G:
Como a única força que produz momento sobre o centro de massa é a força de atrito (já que a gravidade atua diretamente no centro de massa, o que não produz momento em relação ao centro de massa), a equação ficará:
Sendo que é perpendicular a r.
Passo 3
E por fim vamos colocar um referencial onde x está paralelo ao plano inclinado, e y perpendicular, dessa forma, a segunda lei de Newton para a coordenada y será zero:
E as forças envolvidas serão:
O cosseno aparece por precisarmos da projeção da força gravitacional na direção de y, e o 4 é devido às 4 barras, cada uma com massa m.
E para a coordenada x:
Isolando :
Passo 4
Como não há deslizamento, podemos relacionar a aceleração angular à linear pela equação:
substituindo que obtemos antes:
Colocando na equação da força de atrito que encontramos no passo acima:
Isolando de novo:
Substituindo :
Simplificando:
Passo 5
Pela equação da força de atrito, podemos encontrar o coeficiente de atrito estático:
Utilizando a equação de N que encontramos pela segunda lei de Newton para a coordenada y: