Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 215
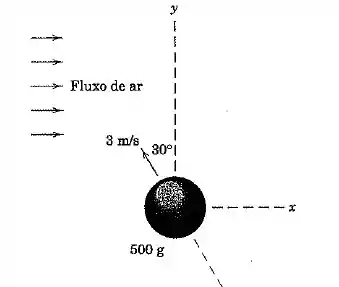
A esfera de está se deslocando no plano horizontal com uma velocidaed de na direção mostrada e encontra um fluxo constante de ar na direção . Se o fluxo de ar exerce uma força essencialmente constante de sobre a esfera na direção , determine o tempo necessário para a esfera cruzar o eixo novamente.
Passo 1
Bom galera, nesse exercício queremos encontrar o tempo necessário para a esfera cruzar o eixo . Sabemos que
Passo 2
Substituindo, temos
Resolvendo a integral e isolando , temos
Passo 3
Por definição, sabemos que
Integrando ambos os lados, ficamos com
Resolvendo essa equação, temos que o tempo é
Resposta
Exercícios de Livros Relacionados
Um sistema de evacuação de emergência para astronautas na torre de lançamento consiste em um longo cabo de deslizamento, abaixo do qual a gaiola de salvamento se desloca para uma distância segura da t
O ônibus espacial lança um satélite de 800k g ejetando-o a partir do compartimento de carga como mostrado. O mecanismo de ejeção é ativado e permanece em contato com o satélite por 4s para fornecer um
Uma nave espacial no espaço profundo está programada para aumentar sua velocidade por uma quantidade desejada ∆ v através da combustão de seu motor por um determinado tempo de duração t . Após vinte e
A força P , que é aplicada ao bloco de 10k g inicialmente em repouso, varia linearmente com o tempo conforme indicado. Se os coeficientes de atrito estático e dinâmico entre o bloco e a superficie hor
O carrinho de 10k g está parado no instante de tempo t = 0 e posteriormente é submetido à força senoidal F = b + 45 s e n ( 6 t ) , onde F e b são expressos em newtons e o tempo t é expresso em segund