Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 124

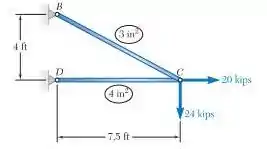
Cada elemento da treliça é mostrada é feito de aço e tem uma área de seção transversal conforme apontado. Usando E = 29 × 10 6   p s i , determine a energia de deformação .

Passo 1

Fala, galerinha. Beleza? Bora pra mais uma questão.

Primeiro, vamos encontrar o comprimento da treliça. Para isso, vamos utilizar o teorema de Pitágoras. Fica assim:

L B C 2 = L D C 2 + 4 2 L B C = 7,5 2 + 4 2 L B C = 102   i n

Em seguida, a partir das equações de equilíbrio, vamos determinar as que atuam nas treliças, temos:

∑ F y = 0 4 8,5 F B C - 24 = 0 F B C = 51   k i p s

E também:

∑ F x = 0 - F C D - 7,5 8,5 51 + 20 = 0 F C D = - 25   k i p s

Opa, agora que encontramos as forças e o comprimento da treliça, bora encontrar a energia de deformação.

Passo 2

Com isso, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação para treliça. Fica assim:

U = F B C 2 L B C 2 E A B C + F C D 2 L C D 2 E A C D

E então basta substuirmos valores. Para a carga, vamos utilizar a menor carga que encontramos no passo anterior, logo:

U = 51 2 102 2 29 3 + 25 2 90 2 29 4 U = 1,767   i n ∙ k i p

É isso, galerinha. Terminamos mais uma questão. Bora fazer mais?

Resposta

U = 1,767   i n ∙ k i p

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o módulo de resiliência para cada uma das seguintes ligas:Monel (trabalhado a frio): E = 180G P a ; σ e = 585M P a Monel (recozido): E = 180G P a ; σ e = 220M P a Liga de titânio: E = 115G
Determinar o módulo de resiliência para cada um dos seguintes metais:Aço inoxidável (laminado a frio): E = 190G P a ; σ e = 520M P a Aço inoxidável (temperado): E = 190G P a ; σ e = 260M P a Ferro fun
Determinar o módulo de resiliência para cada uma das seguintes ligas de alumínio:1100-H14; E = 70G P a ; σ e = 100M P a 2014-T6; E = 75G P a ; σ e = 400M P a 7075-T6; E = 72G P a ; σ e = 500M P a
O diagrama tensão-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de um aço estrutural. Usando E = 200G P a , determinar:o módulo de resil
O diagrama carga-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de uma barra de aço estrutural com 16m m de diâmetro. Sabendo-se que a deformação foi tomada u