Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 4
Determinar o módulo de resiliência para cada um dos seguintes metais:
- Aço inoxidável (laminado a frio):;
- Aço inoxidável (temperado): ;
- Ferro fundido maleável:;
Passo 1
Oi, galera! A vida está agitada? Tudo muito corrido? Então reduz a marcha, porque agora a gente vai resolver uma questão com bastante calma deixando tudo explicadinho.
O exercício quer que a gente calcule quanto vale o módulo de resliliência de três tipos de metais: aço inoxidável (laminado a frio), aço inoxidável (temperado) e ferro fundido. O módulo de resiliência de qualquer material é igual à área embaixo da reta de um diagrama tensão-deformação . Esse diagrama e os dados que a questão nos informa para calcular são mostrados abaixo.
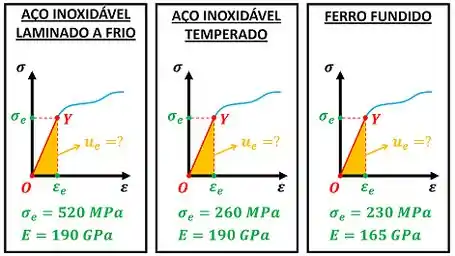
é a tensão de escoamento do material. é o módulo de elasticidade do material. é a deformação a partir da qual o material começa a escoar.
Para calcular o módulo de resilência dos metais, precisamos usar uma equação que relacione os dados que temos ( e ) com o dado que queremos . Essa é a equação abaixo.
Essas são todas as informações que precisamos para resolver a questão e calcular . No próximo passo começaremos os cálculo pelo módulo de resiliência do aço inoxidável (laminado a frio).
Passo 2
Nesse passo nós vamos calcular o módulo de resiliência do aço inoxidável (laminado a frio),.
Mas par fazer isso corretamente, não podemos só pegar os dados e jogar na fórmula!
Antes de tudo a gente precisa colocar o e o nas unidades certas!
Agora sim podemos fazer a substituição dos dados na fórmula!
Passo 3
Nesse passo nós vamos calcular o módulo de resiliência do aço inoxidável (temperado).
Antes, vamos converter a unidade de e de !
Substituindo esse valor na equação de , achamos:
Passo 4
Por fim, vamos calcular o módulo de resiliência do ferro fundido.
Antes disso, temos, novamente, que converter a unidade de e !
Substituindo esse valor na equação de , achamos: