Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 8
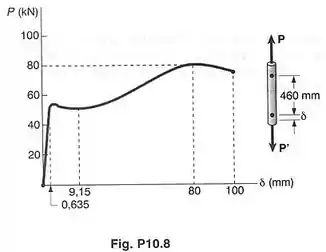
O diagrama carga-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de uma barra de aço estrutural com de diâmetro. Sabendo-se que a deformação foi tomada usando um comprimento de medição igual a , determinar por meio aproximado:
- o módulo de resiliência da liga;
- o módulo de tenacidade da liga.
Passo 1
Oier! Prontos para se aventurar em mais uma questão de método de energia?
O exercício quer que a gente calcule o valor módulo de resliliência e do módulo de tenacidade de uma barra de aço. O módulo de resiliência de qualquer material é igual à área embaixo da reta de um diagrama tensão-deformação . Já o módulo de tenacidade é toda a área sob a curva do diagrama tensão-deformação .
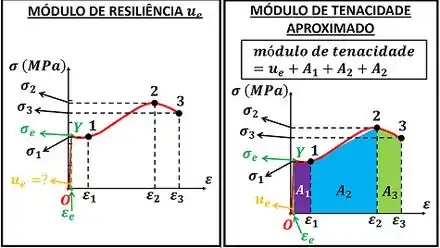
é a tensão de escoamento do material. , e são as taxa deformação da barra de aço nos pontos 1, 2 e 3 respectivamente. , e são as tensões sobre a barra nos pontos 1, 2 e 3. , e são as áreas do trapézios usados para estimar o módulo de tenacidade.
e o módulo de tenacidade são essas áreas do diagrama tensão-deformação.
Mas então como calcularemos eles dois, se o enunciado da questão só nos deu o diagrama carga-deformação?
Refazendo a pergunta: nós temos um diagrama com a força (também chamada de carga ) sobre a barra e a deformação , mas queremos calcular a tensão sobre a barra e a sua taxa de deformação . Como fazemos isso?
Através das fórmulas abaixo!
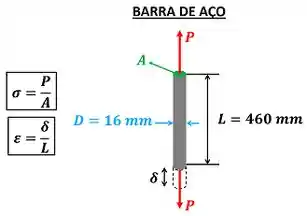
é o comprimento da barra que vale segundo o enunciado.
é a área da seção transversal da barra que pode ser calculada através do diâmetro da barra. Atenção! Não confunda essa área com as área , e dos trapézios!
A carga pode ser encontrada através do diagrama carga-deformação do enunciado!
Então bora calcular as tensões e as taxas de deformação no próximo passo.
Passo 2
Nesse passo, vamos calcular as tensões e as taxas de deformação necessárias para a gente achar e o módulo de tenacidade.
Para encontrarmos os valores de carga e deformação que precisamos, precisamos olhar o gráfico de carga-deformação.
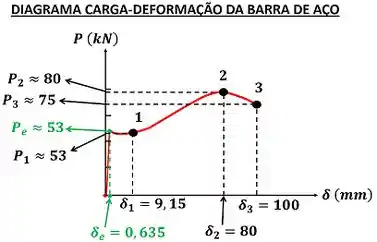
é a deformação da barra, quando ele começa a escoar. , e são as deformações da barra nos pontos 1, 2 e 3. é a carga que faz a barra começar a escoar. , e são as cargas da barra nos pontos 1, 2 e 3.
Pra converter essas cargas e essas deformações , usamos as fórmulas de e .
Quando usamos a carga em e a área em , achamos as tensões em .
Com esses valores de e poderemos enfim calcular o módulo de resiliência no passo seguinte!
Passo 3
Nesse passo, resolveremos a letra (a)! Para calcular , precisamos saber quanto vale a tensão de escoamento da liga, porque é a altura do triângulo que forma a área sob a reta ! A base desse triângulo é igual a .
A figura abaixo mostra a área exagerada do triângulo que fica abaixo de .
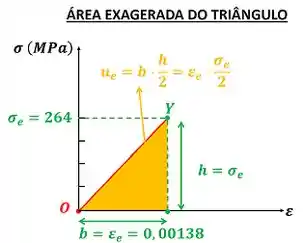
Antes de utilizar , temos que converter essa tensão de para , multiplicando a tensão por .
Substituindo esses valores na fórmula de presente no gráfico, achamos:
Podemos converter esse resultado de para , dividindo por .
Aeee! Achamos a resposta da letra (a)! No próximo passo a gente pode calcular o módulo de tenacidade.
Passo 4
Nesse passo, resolveremos a letra (b) da questão!
O módulo de tenacidade é toda a área sob a curva do diagrama tensão-deformação. Ou seja, para achar esse valor, temos que achar as áreas , e dos trapézios. A fórmula da área do trapézio é base maior mais base menor , vezes altura do trapézio dividido por .
No caso do trapézio, a altura não são valores de tensão , mas sim diferenças entre valores de deformação . As tensões são as bases e . Esses valores de tensão que representam as bases e do trapézio são aproximações encontradas a partir do gráfico.
Isso fica mais claro olhando para a figura abaixo.
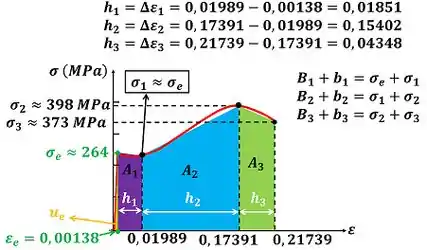
Antes de utilizar as informações da figura, temos que converter as tensões de para , multiplicando a tensão por .
Agora sim, usando as informações presentes na figura, achamos:
Cuidado! O valor de que devemos colocar na fórmula do módulo de tenacidade deve estar em !
Como o módulo de tenacidade é a soma de todas as áreas, encontramos: