Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 50

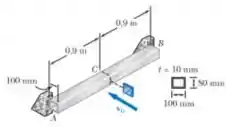
Um tubo de alumínio com a seção transversal mostrada é atingido diretamente na sua seção média por um bloco de 6kg movendo-se na horizontal com uma velocidade de 2m/s. Utilizando E = 70 GPa, determine (a) a carga estática equivalente, (b) a tensão máxima na viga, (c) a deflexão máxima no ponto médio C da viga.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Energia cinética:

T = 1 2 m v 0 2 = 1 2 ( 6 k g ) ( 2 m / s ) ² = 12 J

Momento de inércia.

Alumínio E   =   70   G P a

I a a = 1 12   80 × 100 3 - 60 × 80 3

= 4,1067 × 10 6 m m 4

= 4,1067 × 10 - 6 m 4

Passo 2

Do Apêndice D:

y m = P m L 3 48 E I

U m = 1 2 P m y m = P ² m L 3 96 E I

(a)

U m = T : P 2 m 1,8 3 96 ( 70   G P a ) ( 4,1067 × 10 - 6 m 4 ) = 12   J                 P m = 7535,5   N

P m = 7,54   k N

Passo 3

(b)

M m = 1 4 P m L = 1 4 7535,5   N 1,8 m = 3391   N ∙ m

σ m = M m c I = 3391   N ∙ m 0,050   m 4,1067 × 10 - 6 m 4 = 41,28   M P a

σ m = 41,3   M P a

Passo 4

(c)

y m = P m L 3 48 E I = 7535,5   N 1,8 m 3 48 ( 70   G P a ) ( 4,1067 × 10 - 6 m 4 ) = 3,184 × 10 - 3 m

y m = 3,18 m m

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de (a) P m = 7,54   k N ; (b) σ m = 41,3   M P a e (c) y m = 3,18 m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Usando E = 200G P a , determine a energia de deformação devido à flexão para a barra de aço e o carregamento mostrado. (Desconsidere os efeitos das tensões de cisalhamento.)
Considerando que a viga prismática AB tem uma seção transversal retangular, mostre que para a carregamento indicado o valor máximo da densidade de energia de deformação na viga é M m a z = 45 8 U V Em