Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 35

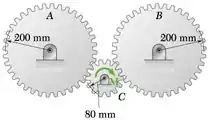
Cada uma das engrenagens A e B tem massa de 10 kg e um raio de giração de 150 mm; a engrenagem C tem uma massa de 2,5 kg e um raio de giração de 60 mm. Se o binário M de intensidade constante 6 N · m é aplicada à engrenagem C, determine (a) a aceleração angular da engrenagem A, (b) a força tangencial que a engrenagem C exerce na engrenagem A.

Passo 1

Cinemática:

Expressamos que os componentes tangenciais das acelerações dos dentes da engrenagem são iguais:

a t = 10 α A = 10 α B = 4 α C

a B = α A

α C = 2.5 α A

Passo 2

Cinética:

Engrenagem A:

I - A = m A k - A 2 = 20 32.2 7.5 12 2 = 0.24262   lb ∙ s 2 ∙ ft

+ Σ M A = Σ M A eff :               F 10 12 = 0.24262 α A

F = 0.29115 α A

Por causa da simetria, a engrenagem C exerce uma força igual F na engrenagem B.

Passo 3

Engrenagem C:

I - C = m C k - C 2 = 5 32.2 3 12 2 = 0.009705   lb ∙ s 2 ∙ ft

+ Σ M C = Σ M C eff :               M - 2 F r C = I - C α C

50 12 lb ∙ ft - 2 F 4 12 ft = 0.009705 α C

Passo 4

  1. Aceleração angular da engrenagem A:

    2. Substituindo α C de (1) e a forma F (2):

    4.1667 - 2 0.29115 α A 1 3 = 0.009705 2.5 α A

    4.1667 - 0.19410 α A = 0.02426 α A

    4.1667 = 0.21836 α A

    α A = 19.081   rad/ s 2

    Passo 5

  2. Força tangencial F.

Substituindo para α A em (2):

F = 0.29115 19.081

Resposta

a )   α = 19.08   rad/ s 2  

b )   F A = 5.56   lb ↗

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco de concreto P está sendo abaixado pelo arranjo de cabo e polia mostrado. Se os pontos A e B têm velocidades de 0,4m / s e 0,2m / s , respectivamente, calcule a velocidade de P , a velocidade d
O cursor A se desloca na ranhura horizontal com uma velocidade constante v por um curto intervalo de movimento. Determine a velocidade angular ω da barra A B em termos do deslocamento x A .
A roda está rolando sem deslizar com uma velocidade angular ω . Admitindo que a linha P O C gire através de um ângulo diferencial d θ durante um intervalo de tempo d t , mostre que a velocidade do pon
No Problema, a junta rotulada entre a barra e o colar A é substituída por um grampo em U como mostrado na figura. Determine, (a) a velocidade angular da barra, (b) a velocidade do colar A.
No Problema, a velocidade do ponto B é conhecida e é constante. Para a posição mostrada na figura, determine (a) a aceleração angular do braço guia, (b) a aceleração do ponto C.