Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 27
O cursor se desloca na ranhura horizontal com uma velocidade constante por um curto intervalo de movimento. Determine a velocidade angular da barra em termos do deslocamento .
Passo 1
A velocidade angular será igual à derivada de no tempo, , conforme mostra a figura a seguir:
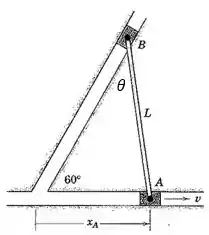
Então, podemos aplicar a lei dos senos no triângulo da figura:
Passo 2
Podemos derivar em relação ao tempo a equação que acabamos de encontrar, obtendo:
Porém, , então:
Passo 3
Como queremos apenas em função de , e não de , temos que substituir por outra expressão. Pra isso, podemos voltar na equação obtida no :
Pela relação fundamental da trigonometria:
Logo,
Resposta
Exercícios de Livros Relacionados
27. Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 450 t 2 + 60r a d / s 2 , onde t é dado em segundos. Determine a velocidade angular e o
39. Determine a velocidade e a aceleração da plataforma P como uma função do ângulo θ do came C se o came gira com uma velocidade angular constante ω . O pino de conexão não interfere no movimento de
46. No instante que θ=30°, a manivela AB gira com uma velocidade angular e aceleração angular de ω=10rads e α=2rads2, respectivamente. Determine a velocidade e aceleração do bloco deslizante C nesse i
38. O bloco se descola para a esquerda com uma velocidade constante v 0 . Determine a velocidade angular e aceleração angular da barra como uma função de θ .
53. No instante mostrado, o disco está girando com uma velocidade angular ω e tem uma aceleração angular α . Determine a velocidade e aceleração do cilindro B nesse instante. Despreze a dimensão da po