Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 31

O bloco de concreto P está sendo abaixado pelo arranjo de cabo e polia mostrado. Se os pontos A e B têm velocidades de 0,4   m / s e 0,2   m / s , respectivamente, calcule a velocidade de P , a velocidade do ponto C para o instante representado, e a velocidade angular da polia.

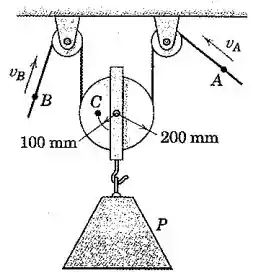
Passo 1

Pelo vínculo geométrico da polia, temos:

v A + v B = 2 v P

v P = v A + v B 2

v P = 0,4 + 0,2 2

v P = 0,3   m / s

Passo 2

Para calcular a velocidade angular ω , perceba que a velocidade v P é a velocidade de translação da polia, que deve ser somada (vetorialmente) com a velocidade de rotação ω r para se obter a velocidade resultante de um determinado ponto que dista r do centro da polia.

Então, por exemplo, na extremidade direita da polia, temos uma velocidade resultante igual à velocidade da corda v A , para baixo. Esse sentido coincide com o da velocidade de translação e de rotação, logo:

v A = v P + ω R

ω = v A - v P R

ω = 0,4 - 0,3 0,200

ω = 0,5   r a d / s

Passo 3

Agora, perceba que a velocidade do ponto C vai ser a soma vetorial da velocidade de rotação (para cima) e da velocidade de translação (para baixo). Então:

v C = - ω r + v P

v C = - 0,5 0,100 + 0,3

v C = 0,25   m / s

Resposta

v P = 0,3   m / s

v C = 0,25   m / s

ω = 0,5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cursor A se desloca na ranhura horizontal com uma velocidade constante v por um curto intervalo de movimento. Determine a velocidade angular ω da barra A B em termos do deslocamento x A .
A roda está rolando sem deslizar com uma velocidade angular ω . Admitindo que a linha P O C gire através de um ângulo diferencial d θ durante um intervalo de tempo d t , mostre que a velocidade do pon
O cursor A se desloca com velocidade constante v sobre a reta guia por um curto intervalo, enquanto o cursor B se desloca sobre a guia circular cujo centro está em O . Determine a velocidade angular ω
O ponto A recebe uma aceleração constante a para a direita a partir do repouso com x essencialmente nulo. Determine a velocidade angular ω da barra A B em termos de x e a .
28. . Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 50 ω 0,5r a d / s 2 , onde w é dado em rad/s. Determine a velocidade angular e o deslo