Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 49
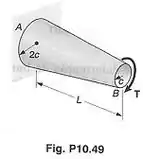
Mostrar, por integração, que a energia de deformação da barra , em forma de tronco de cone, é
onde é o momento de inércia polar da seção transversal da barra, na extremidade .
Passo 1
Fala, pessoas! Estão de bem com a vida? Então partiu resolver uma questão de energia de deformação?
Antes de começar, eu tenho uma notícia triste! O enunciado está errado! Mais precisamente, a equação de do enunciado está errada! A equação certa se encontra abaixo.
Essa questão quer que a gente mostre como se chega na fórmula que calcula a energia de deformação de uma barra com seção transversal de área que varia.
Conseguimos fazer isso, resolvendo a integral abaixo.
onde é o módulo de elasticidade transversal da barra, é o momento de inércia polar de cada seção transversal da barra e é o torque ao qual a barra está submetida!
Antes de resolver essa integral, precisamos determinar quanto vale .
Passo 2
Para entender quanto vale , precisamos lembrar da fórmula de para áreas circulares.
onde é o raio do tronco de cone em uma posição do tronco. A figura abaixo mostra o raio .
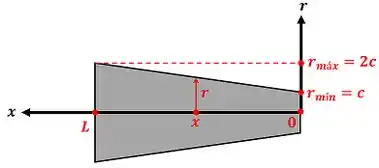
Como podemos ver, o raio varia linearmente com . Isso quer dizer que a equação de é uma reta! Dessa forma, somos capazes de achar essa equação a partir da equação da reta.
é a inclinação da reta. Ela é igual a variação de dividida pela variação de .
é valor de , quando . Logo:
Substituindo e na equação de , achamos:
Substituindo essa equação de , na equação de , encontramos o valor do momento polar.
Sabendo quanto vale , podemos começar a resolver a integral de .
Passo 3
Nesse passo a gente vai encontrar , resolvendo a integral. Para isso, substituímos o que achamos no passo anterior na integral.
Como , , e são constantes, podemos tirar eles da integral.
Resolvendo a integral, encontramos:
Calma! Ainda não é hora de comemorar! Achamos a energia de deformação , mas ela ainda não está em função do momento de inércia polar mínimo .
Passo 4
O momento de inércia é o momento de inércia da seção transversal de raio . Usando essa informação na fórmula de para áreas circulares, achamos:
Substiuindo o presente na fórmula de por , vamos conseguir chegar onde a questão pede!
Resposta
Ei, a resposta está no passo a passo :)