Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 14
Cada uma das quatro hastes verticais, ligadas às duas barras horizontais, tem uma seção transversal uniforme de e os pinos tem diâmetro de 14 mm. Determine o máximo valor da tensão normal média, causada pela carga de , nas hastes conectadas pelos (a) pontos B e E; (b) pontos C e F. Assuma que a carga de 24 kN aponta para cima.
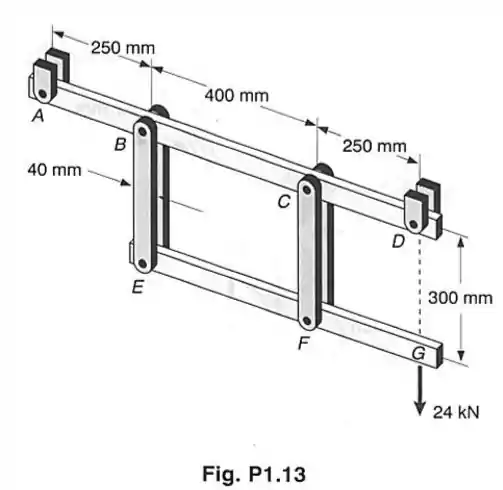
Passo 1
Neste problema vamos ter que achar as forças atuantes nas hastes BE e CF e, com a área transversal dessas hastes, achar a tensão normal.
Mas cuidado porque esse exercício pediu a tensão normal máxima, ou seja, temos que considerar o ponto onde as hastes são perfuradas pelo pino de de diâmetro!
Vamos lembrar também que as hastes são DUPLAS logo a força atuante em cada uma delas terá de ser dividida por 2.
Passo 2
Vamos achar as forças atuantes nas hastes fazendo o diagrama de corpo livre da barra EFG:
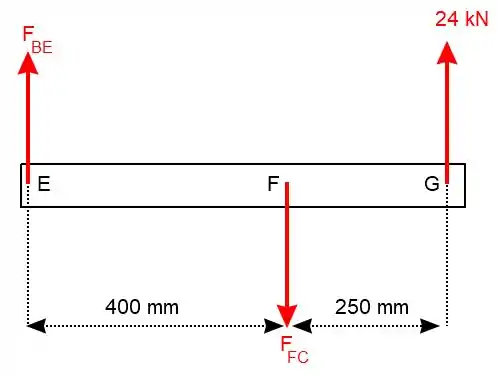
Agora vamos ter que aplicar o somatório de momentos e o somatório das forças em para achar as forças e :
Considerando o sentido horário positivo:
Considerando o eixo positivo para cima:
Passo 3
Vamos calcular a área das hastes, da só uma olhada em como é a seção transversal de cada haste no ponto mais crítico, que é onde o pino passa:
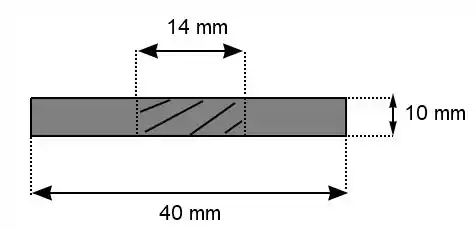
Então a gente tem que desconsiderar a área marcada com os traços porque é onde o pino passa e ali não há resistência da haste pelo fato de ser um furo.
Logo a área efetiva é:
Passo 4
Agora basta substituir na equação da tensão normal, para a haste BE vamos ter:
Mas lembra que a haste é dupla?! Logo a força não será apenas será
Como a área é
Passo 5
Agora basta substituir na equação da tensão normal, para a haste FC vamos ter:
Assim como na letra A a haste é dupla. Logo a força não será apenas será
Como a área é
Passo 6
Este problema é exatamente o mesmo do anterior a única diferença é que neste as hastes BE e FC estão sob compressão e tração, respectivamente. Já no anterior era o contrário a haste BE estava sob tração e a FC sob compressão.
Vamos pegar o exemplo da haste BE deste exercício, a força que calculamos no passo 2 é a força que a barra EFG faz na haste BE. Pode-se ver que essa é uma força que acaba por comprimir a haste BE, que está, portanto, em compressão.
Resposta
a)
b)