Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 144
Cada um dos suportes de pouso de uma espaçonave de exploração de planetas é projetado como uma treliça espacial simétrica em relação ao plano x-z vertical, conforme mostrado. Para uma força de aterrissagem F = 2,2 kN, calcule a força correspondente no membro BE. A suposição de equilíbrio estático para a treliça é permitida se a massa da treliça for muito pequena. Assuma cargas iguais nos membros posicionados simetricamente.
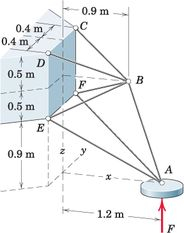
Passo 1
Uma vez que a treliça e o carregamento são simétricos ao plano xOz, as forças nos membros AE e AF são iguais, bem como as forças nos membros BE (BD) e BF (BC)
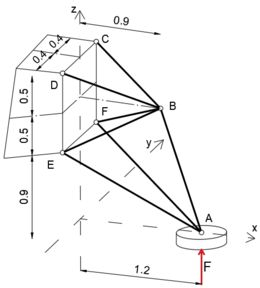
Podemos escrever o vetor de força como um produto de sua magnitude AE e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e E são
Passo 2
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Podemos escrever o vetor de força como um produto de sua magnitude AF e um vetor unitário de direção de força
Passo 3
Podemos ver na imagem que as coordenadas dos pontos A e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 4
Podemos escrever o vetor de força como um produto de sua magnitude AB e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos A e B são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 5
Podemos notar que a força de 2,2 kN é paralela ao eixo z, portanto, podemos escrevê-la como
Ao analisar a junta A, podemos determinar o membro de força AB
Presumimos que todos os membros estão em tensão
Agora temos três equações de equilíbrio
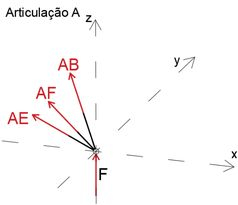
Passo 6
Uma vez que as forças AE e AF são iguais, podemos escrever a equação (1) como
Podemos expressar as forças AE e AF em função de AB
Agora podemos substituir AE e AF por 0,136AB na equação (3), a fim de determinar a força no membro AB
Passo 7
Agora podemos escrever o vetor como
Observe que o vetor é oposto ao vetor , então podemos escrevê-lo como
Ao analisar a junta B e usando simetria, podemos determinar a força no membro BE
Passo 8
Mais uma vez, assumimos que todos os membros estão em tensão
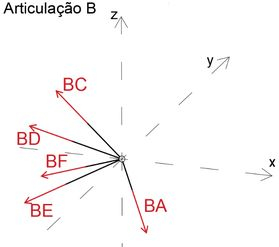
Podemos escrever o vetor de força como um produto de sua magnitude BC e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e C são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Podemos escrever o vetor de força como um produto de sua magnitude BD e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e D são
Passo 9
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Podemos escrever o vetor de força como um produto de sua magnitude BE e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e E são
Passo 10
Uma vez que sabemos dois pontos na linha de ação, podemos escrever como
Podemos escrever o vetor de força como um produto de sua magnitude BF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos B e F são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 11
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos três equações de equilíbrio
Passo 12
Uma vez que sabemos por simetria que as forças BC e BD são iguais, bem como as forças BE e BF, podemos escrever a equação (4) como
Multiplicando-o por , teremos
Também podemos escrever a equação (6) como
Finalmente, adicionando as equações (7) e (8), podemos determinar a força BE