Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 149
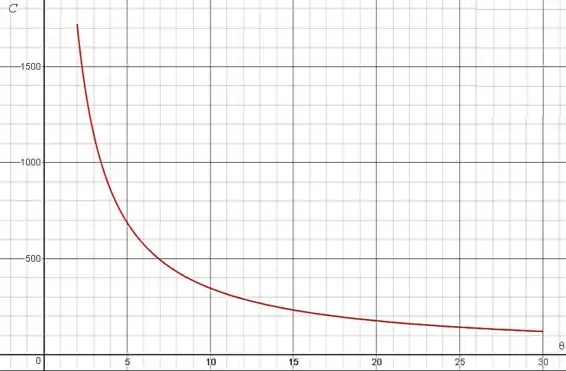
Para uma dada força P no manípulo do grampo articulado, a força de aperto C aumenta para valores muito grandes à medida que o ângulo diminui. Para P = 30 lb, determine a relação entre C e e plote-a como uma função de de a . Suponha que o eixo deslize livremente em sua guia.
Passo 1
Primeiro, podemos ver que o ângulo entre para P e vertical também é .
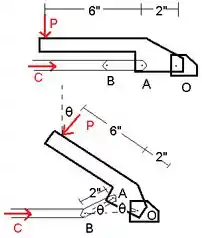
Se isolarmos a alça que está em equilíbrio, podemos calcular a força no membro AB.
Passo 2
Finalmente, se isolarmos o eixo da braçadeira, que também está em equilíbrio, podemos obter a força C.
Também temos que mudar a direção do AB, pois agora estamos vendo como ele age no ponto B.
Gráfico C-
Resposta
Exercícios de Livros Relacionados
Determine as forças nos membros CH, AH e CD da treliça carregada.
O conjunto da roda do nariz é elevado pela aplicação de um torque M para ligar BC através do eixo em B. Se o braço e a roda AO têm um peso combinado de 100 lb com centro de gravidade em G, encontre o
Todos os membros de duas forças da treliça carregada têm o mesmo comprimento. O membro BCD é uma viga rígida. Determine as forças nos membros BG e CG em termos da carga L.
Se for conhecido que o pino central A suporta metade da carga vertical mostrada, determine a força no membro BF.
O caçador de árvores corta árvores grandes perto do nível do solo e continua a agarrar o tronco. Determine a força no cilindro hidráulico AB para a posição mostrada se a árvore pesar 6000 lb. Determin