Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 91
Cada uma das três vigas de aço laminado mostradas (numeradas por e) destinam-se a suportar ações uniformemente distribuídas de . O vão livre de cada uma dessas vigas é de e são suportadas por duas vigas mestras e de aço laminado de . Sabendo que a tensão normal admissível para o aço utilizado é igual a 24 , selecione o perfil mais econômico para as três vigas, o perfil de mesas largas mais econômicos para as duas vigas mestras.
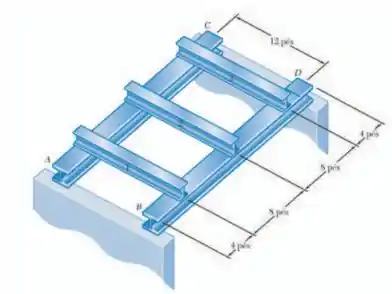
Passo 1
Fala aí, pessoal. Beleza? Bora zerar esse livro.
Este problema nos pede para selecionar o perfil mais econômico que suporta o carregamento dado. Primeiro, bora esboçar o DCL para as vigas e:
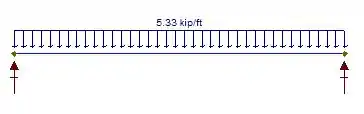
Sabendo disso, vamos calcular a reação de apoio através das equações de equilíbrio:
Por simetria, temos que , logo:
Assim, podemos concluir esboçar o diagrama força cortante:
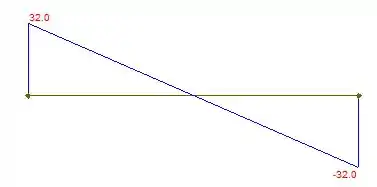
E também o diagrama de momento fletor:
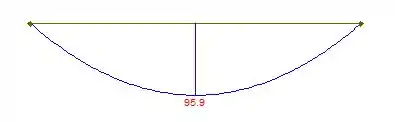
Assim, podemos ver que o momento máximo absoluto é:
Passo 2
Em seguida, já que temos o momento máximoe o enunciado nos forneceu a tensão normal admissível . Então, basta encontrarmos a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
E então, para determinarmos o perfil mais econômico devemos olhar no ábaco o valor mínimo admissível do módulo de resistência imediamente maior que o que encontramos. Assim, o perfil escolhido é:
Que possui .
Passo 3
Agora que determinamos o perfil para as vigas de cima, vamos repetir o processo para determinarmos o perfil para as vigas mestras. Então, bora esboçar o DCL:
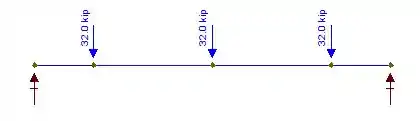
Em seguida, vamos calcular a reação de apoio através das equações de equilíbrio:
Por simetria, temos que , logo:
Assim, podemos esboçar o diagrama força cortante:
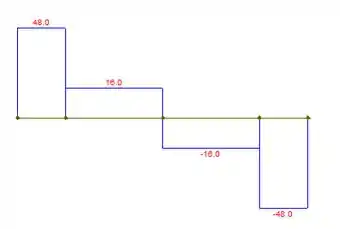
E também o diagrama de momento fletor:
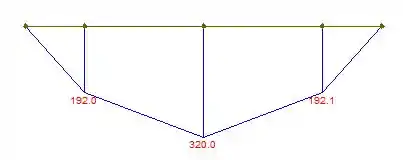
Assim, podemos ver que o momento máximo absoluto é:
Passo 4
Agora que temos o momento máximoe o enunciado nos forneceu a tensão normal admissível , basta encontrarmos a outra variável da qual a tensão normal depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
Novamente, vamos até o ábaco para encontrar o valor mínimo admissível do módulo de resistência imediamente maior que que encontramos. Portanto, o perfil escolhido é:
Que possui .
É isso, galera! Bora fazer mais exercícios pra ficar craque.