Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 22
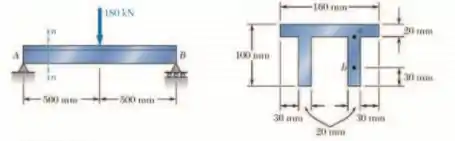
Para a viga e o carregamento mostrado, considere a seção n-n e determine o tensão de cisalhamento em (a) ponto a, (b) ponto b.
Passo 1
E ai gurizada tudo beleza? O enunciado pede que a gente determinar determine o tensão de cisalhamento em (a) ponto a, (b) ponto b ... .... Então partiu!
Começaremos calculando a inércia da seção dos elementos divididos como:
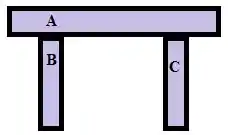
Considerando a força cortante V= 90 KN , vamos determinar Y e a inércia respectivamente :D
Para a inércia temos:
Passo 2
Determinando a área temos:
Considerando y= 25 mm temos:
Calculando a tensão de cisalhamento temos:
Passo 3
Determinando a área temos:
Considerando y= 65-15=50 mm temos:
Calculando a tensão de cisalhamento temos:
Resposta
Exercícios de Livros Relacionados
A força vertical 5 kN é aplicada ao aro, de um disco de raio igual a 120 mm, como mostrado. Sabendo-se que o eixo AB tem o diâmetro de 80 mm, determinar as tensões normal e de cisalhamento no ponto H.
A barra AB é conectada, através de juntas esféricas, ao colar A ao disco de raio 90 mm. O disco é soldado ao tubo DE, que tem um diâmetro externo de 80 mm e uma espessura igual a 6 mm. Sabendo-se que
Para o sistema do Prob 5.70 determinar as tensões, normal e de cisalhamento, no ponto K.
Duas forças de 4 kN são aplicadas ao elemento de máquina AB, como mostrado. Determinar as tensões, normal e de cisalhamento, no: (a) ponto a; (b) ponto b; (c) ponto c.
Duas forças de 4 kN são aplicadas ao elemento de máquina AB, como mostrado. Determinar as tensões, normal e de cisalhamento, no: (a) ponto d; (b) ponto e; (c) ponto f.