Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 108
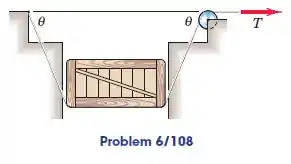
A caixa uniforme de massa é suportada pela tensão na tira flexível passando por baixo dela. Para dada posição, determine uma expressão para a tensão na cinta necessária para começar (a) a subida da caixa e (b) descida da caixa se o coeficiente de fricção entre a correia e a caixa é. Negligencie qualquer atrito entre a caixa e suas guias verticais.
Passo 1
Precisamos de uma expressão para que represente a subida e a descida da caixa.
O coeficiente mínimo de atrito entre o cabo e a polia é dado por:
Ou:
Onde é a tensão na corda no lado tenso e no lado frouxo.
Substituindo os respectivos valores, temos que:
Passo 2
Para levantar o peso, temos que a condição de trabalho deve ser:
Substituindo os dados, temos que:
Passo 3
No momento da descida, a ordem das tensões é invertida, e representa o lado frouxo, logo:
Realizando o mesmo procedimento do passo anterior, temos que:
Substituindo os dados, temos que: