Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 30

Repita Prob. 28/06, mas agora o carro tem tração nas quatro rodas. Suponha que o escorregamento ocorra em A e B simultaneamente.

Passo 1

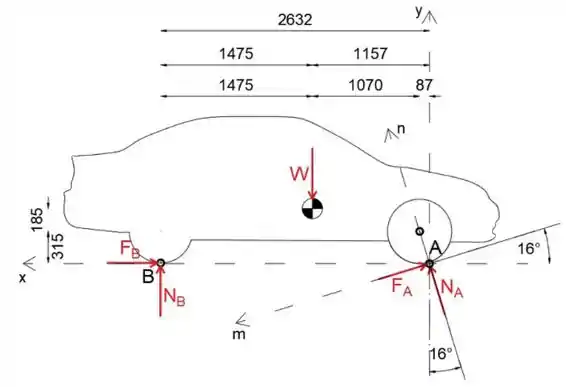
Primeiro, vamos desenhar o diagrama de corpo livre do carro

O peso do carro é

W = m g W = 1600 ⋅ 9.81 W = 15696 N

Observe que, como o raio de uma roda é 315 mm, a distância horizontal entre o centro da roda dianteira e o ponto A é

l = 315 s i n ⁡ 16 ∘ l = 87 m m

Passo 2

Equacionando a soma dos momentos sobre o ponto A a zero, determinaremos a força de reação normal NA

∑ M A = 0

2632 N B - 1157 W = 0 N B = 1157 W 2632 N B = 1157 ⋅ 15696 2632 N B = 6900 N

Observe que o escorregamento ocorre em A e B simultaneamente, portanto, o atrito FB é

F B = μ s ⋅ N B F B = 6900 μ s

Equacionando a soma das forças nas direções m e n a zero, determinaremos as forças FA e NA

∑ F m = 0

- N B s i n ⁡ 16 ∘ - F B c o s ⁡ 16 ∘ + W s i n ⁡ 16 ∘ - F A = 0 F A = - N B s i n ⁡ 16 ∘ - F B c o s ⁡ 16 ∘ + W s i n ⁡ 16 ∘

Substituiremos NB, FB e W por seus valores

F A = - 6900 s i n ⁡ 16 ∘ - 6900 μ s c o s ⁡ 16 ∘ + 15696 s i n ⁡ 16 ∘ F A = 2424 - 6633 μ s                                                                                                                                                             ( 1 )

∑ F n = 0

- F B s i n ⁡ 16 ∘ + N B c o s ⁡ 16 ∘ - W c o s ⁡ 16 ∘ + N A = 0 N A = F B s i n ⁡ 16 ∘ - N B c o s ⁡ 16 ∘ + W c o s ⁡ 16 ∘

Novamente, vamos substituir NB, FB e W por seus valores

N A = 6900 μ s s i n ⁡ 16 ∘ - 6900 c o s ⁡ 16 ∘ + 15696 c o s ⁡ 16 ∘ N A = 8455 + 1902 μ s                                                                                                                                                         ( 2 )

Passo 3

Uma vez que o escorregamento ocorre em A e B simultaneamente, podemos escrever a expressão para o atrito FA como

F A = μ s ⋅ N A

Substituiremos FA e NA pelas expressões (1) e (2) respectivamente

2424 - 6633 μ s = μ s ⋅ 8455 + 1902 μ s 2424 - 6633 μ s = 8455 μ s + 1902 μ s 2

1902 μ s 2 + 15088 μ s - 2424 = 0

Finalmente, determinaremos o coeficiente de atrito mínimo resolvendo a equação quadrática acima

μ s = - 15088 ± 15088 2 + 4 ⋅ 1902 ⋅ 2424 2 ⋅ 1902

μ s = 0.1575

Resposta

μ s = 0.1575

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a altura máxima h em metros à qual a garota pode subir no escorrega sem se apoiar no corrimão ou em sua perna esquerda. O coeficiente de atrito estático entre os sapatos da garota e o escorr
O tambor tem um peso de 500N e repousa sobre o piso para o qual o coeficiente de atrito estático é μ s = 0,6 . Se a = 0,6m e b = 0,9 , determinea menor intensidade da força P que causará a iminência d
O tambor tem um peso de 500N e repousa sobre o piso para o qual o coeficiente de atrito estático é μ s = 0 , 5 . Se a = 0 , 9m e b = 1,2 , determinea menor intensidade da força P que causará a iminênc
Um homem tenta suportar uma pilha de livros horizontalmente aplicando um força compressiva F = 120N uma massa de 0,95k g , determine o maior número de livros que poder ser suportados na pilha. O coefi
O refrigerador tem um peso de 900N ( ≈ 90k g ) e respousa sobre um piso cerâmico para qual μ s = 0,25 . Se o homem empurra horizontalmente o refrigerador no sentido mostrado, determine a menor intensi