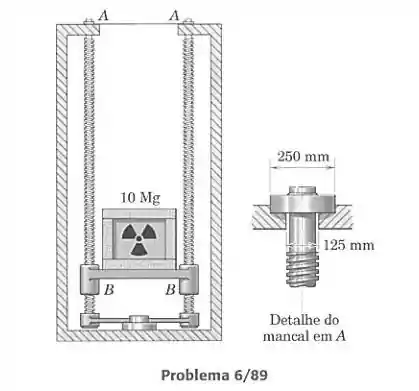
O caixote de 10 Mg é abaixado para uma câmara de armazenamento subterrânea em um elevador de dois parafusos projetado como mostrado. Cada parafuso tem uma massa de 0,9 Mg, um diâmetro médio de 120 mm e uma rosca quadrada simples com um passo de 11 mm. Os parafusos são girados em sincronismo por uma unidade motorizada na base do dispositivo. Toda massa do caixote, dos parafusos e da plataforma de 3 Mg do elevador é sustentada uniformemente por mancais radiais planos em , cada um tendo um diâmetro externo de 250 mm e interno de 125 mm. A pressão nos mancais é considerada uniforme sobre toda a superfície dos mancais. Se o coeficiente de atrito para os mancais radiais e os parafusos em B

Vale 0,15, calcule o torque que deve ser aplicado a cada parafuso para suspender o elevador e para abaixar o elevador.

Vamos calcular os ângulos e . O ângulo pode ser calculado colocando uma parte da rosca que completa uma volta inteira no parafuso em um plano vertical. A distância vertical entre um extremo e outro será o passo mm e a distância horizontal será a circunferência do parafuso, mm:

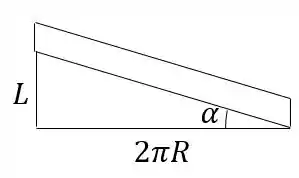
Então achamos através de sua tangente:

O ângulo de atrito é calculado através do coeficiente de atrito, pela fórmula:

Agora vamos calcular o momento feito para se opor ao atrito no mancal. O raio maior do mancal é mm e o raio menor é mm. A força aplicada em cada mancal é a força que suporta o peso do para fuso e de metade do peso da prateleira e da caixa:

Então aplicamos a fórmula:

Agora vamos calcular o momento necessário para levantar o parafuso:

A força aplicada em cada parafuso é a força necessária para levantar a prateleira e a caixa, dividida por 2:

Então o momento necessário para levantar o parafuso é:

Finalmente calculamos o momento necessário pra abaixar o parafuso:

Então o momento necessário para descer o parafuso é: