Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 44
Determine as forças nos elementos e da treliça simétrica carregada.
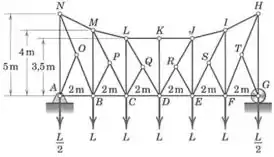
Passo 1
Além das forças de módulo que já estão agindo sobre os pontos e , cada um desses pontos terá que suportar metade das outras forças que agem sobre a treliça, já que ela é simétrica, então:
Passo 2
Nosso primeiro objetivo é encontrar a força . Para isso vamos aplicar o método das seções.
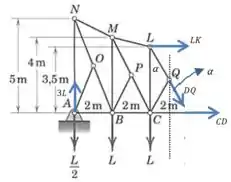
E agora podemos aplicar a condição de equilíbrio na direção vertical:
Onde o ângulo pode ser calculado da seguinte forma:
E então:
Passo 3
Em seguida queremos encontrar a força . Mas dê uma olhada no ponto no desenho, ele só é apoiado por forças em três direções.
Se houvesse uma força em , ela teria uma componente perpendicular às outras duas forças que atuam em , e então não poderia haver equilíbrio!
Resposta
As forças são e .