Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 105
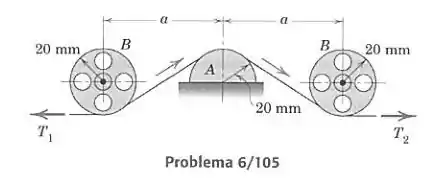
Uma fita magnética passa, à velocidade constante, em torno das polias esticadores leves e sobre a cabeça de gravação circular fixa . A força trativa na fita não varia enquanto ela passa em torno das polias esticadoras. Calcule o espaçamento mínimo , no projeto dessa unidade, para o qual a razão entre as forças trativas e não excederá 1,15. O coeficiente de atrito entre a fita e a cabeça vale 0,10.
Passo 1
Como a fita se move a uma velocidade constante, podemos dizer que ela está em equilíbrio. A fórmula para o equilíbrio de uma fita enrolada em tono de uma superfície é dada a seguir:
Sendo e as trações maior e menor nas extremidades da fita, o coeficiente de atrito entre a fita e a superfície, nesse caso igual a 0,10, e o ângulo total de contato da fita com a superfície. Como queremos o caso limite, onde , nossa equação fica:
E então devemos escolher tal que o ângulo total do contato da fita com com a cabeça satisfaça essa condição. O ângulo é mostrado na figura:
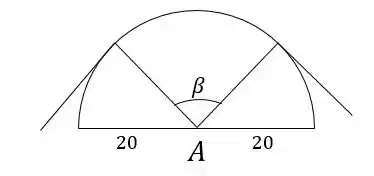
Passo 2
Resolvendo então nossa equação, encontramos o nosso ângulo , em radianos:
Agora devemos achar analisando a geometria do problema:
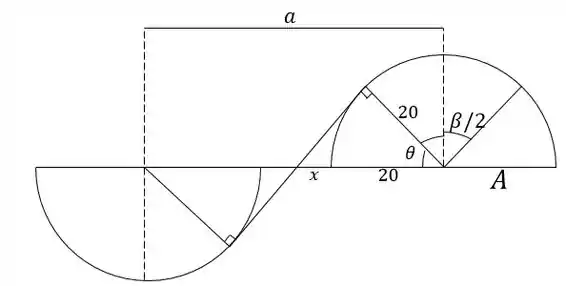
O ângulo da figura em radianos é igual a:
Vamos achar o cosseno de em função de . Primeiro descobrimos a distância :
No triângulo retângulo que contêm , o cateto adjacente ao ângulo é e a hipotenusa é :
Mas como sabemos que :
Com essa relação achamos :