Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 106
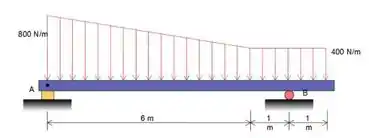
Determine as reações nos apoios da viga carregada como mostrado.
Passo 1
Nesta tarefa, precisamos determinar as reações nos apoios da viga.
Passo 2
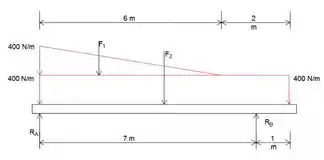
Primeiro, vamos calcular a força F1
Agora, vamos calcular a força F2
Agora, os momentos sobre A
Passo 3
Por fim, consideraremos o equilíbrio das forças horizontais
Resposta
Exercícios de Livros Relacionados
Localize o centro de massa z - do conjunto. O cilindro e o cone são feitos de materiais com densidades de 5M g / m 3 e 9M g / m 3 , respectivamente.
A montagem é feita de um hemisfério de aço, ρ a ç o = 7,80M g / m 3 ç e um cilindro de alumínio, ρ a l = 2,70M g / m 3 . Determine o centro de massa da montagem se a altura do cilindro for h = 200m m
Localize o centro de gravidade ( x - ,y - , z - ) da montagem. Os blocos triangular e retangular são feitos de materiais com pesos específicos de 80k N / m 3 e 32k N / m 3 , respectivamente.
Determine a distância x - até o centroide do sólido que consiste em um cilindro com um furo de profundidade h = 50m m escavado em sua base.
A montegem é feita de um hemisfério de aço, ρ a ç o = 7,80M g / m 3 ç e um cilindro de aluminio, ρ a l = 2,70M g / m 3 . Determine a altura h do cilindro de modo que o centro de massa da montagem este