Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 245
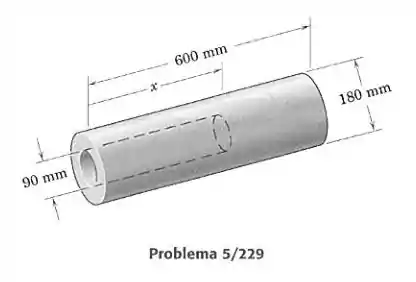
Uma carga homogênea de propelente sólido para um foguete está na forma de um cilindro circular com um furo concêntrico de profundidade . Para as dimensões mostradas, faça um gráfico de , a coordenada do centro de massa do propelente, em função da profundidade do furo desde até mm. Determine o valor máximo de e mostre que ele é igual ao valor correspondente de .
Passo 1
Vamos calcular o centro de massa do propelente através da fórmula para o centro de massa de dois corpos homogêneos combinados:
Nesse caso consideramos como corpo 1 o cilindro maior inteiro, e como corpo 2 a parte vazia, como se fosse um segundo corpo de volume negativo.
Passo 2
Primeiro calculamos o volume do cilindro maior inteiro:
O centro de massa se situa no meio do cilindro:
Passo 3
Agora calculamos o volume do buraco cilíndrico:
O centro de massa fica no meio:
Passo 4
Vamos agora aplicar a fórmula:
Vamos dividir em cima e em baixo por para simplificar:
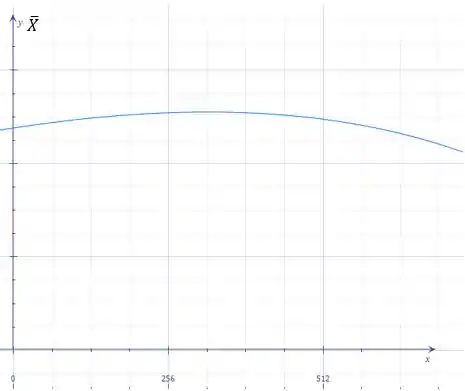
Treçamos então o gráfico de em função de :
Passo 5
Agora vamos maximizar a função . O máximo ocorrerá quando . Vamos então derivar:
Como o denominador é sempre positivo, queremos então o denominador igual a zero. Então:
Resolvemos a equação de segundo grau para encontrar :
Como queremos um valor entre 0 e 600 mm:
O valor de nesse ponto é: