Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 20
Calcule as forças nas barras , e da treliça carregada.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as forças que as barras , e da treliça estão submetidas devido aos carregamentos de exercidos nos pontos e .
Antes de começarmos os cálculos, vamos analisar o problema. Se olharmos o nó , vemos que não há força vertical aplicada no nó para equilibrar a componente vertical da força na barra , então:
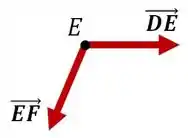
E, consequentemente, a componente horizontal de também é nula, logo:
Passo 2
Para descobrirmos o módulo, direção e sentido das forças atuando nas barras, precisamos sempre partir de um ponto/nó que tenha uma força com módulo, direção e sentido conhecidos.
Agora que sabemos que é nula, vamos analisar o nó :
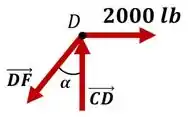
Onde o ângulo é dado por:
Uma vez que a treliça está em equilíbrio, podemos utilizar as equações de equilíbrio de forças nos nós:
Sempre que uma força apontar para o nó ela é de compressão , ou seja, tende a comprimir a barra. Se apontar para fora, ela é de tração e tende a alongar a barra.
Passo 3
Show, feito isso, vamos repetir esse procedimento para alguns outros nós até descobrirmos as forças em todas as barras. Analisando agora o nó , lembrando que .
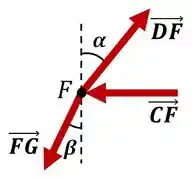
Onde o ângulo é dado por:
Fazendo então o equilíbrio de forças nas direções e , nós temos:
Passo 4
Agora sim: the grand finale!! Hehe
Para encontrar a força na barra que está faltando, vamos analisar o nó :
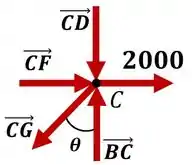
Onde o ângulo é dado por:
E, finalmente, fazendo o equilíbrio de forças na direção :
Ufa! Mas até que não foi tão difícil né? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 