Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 24
A análise do vento agindo em uma pequena igreja havaiana, que resistiu aos ventos de do furacão Iniki em 1992, mostrou que as forças transmitidas a cada painel de treliça do telhado eram as mostradas. Trate a estrutura como uma treliça simétrica simples e despreze qualquer componente horizontal da reação de suporte em . Identifique o membro da treliça que suporta a maior força, tensão ou compressão e calcule essa força.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para identificar a barra da treliça que suporta a maior força devido aos carregamentos aplicados, o módulo dessa força e se ela é de tração ou compressão.
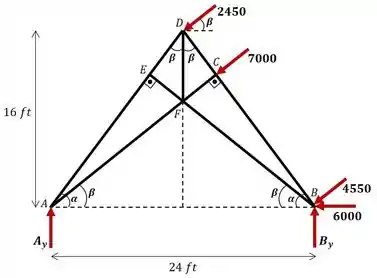
Onde o ângulo é dado por:
E a distância :
Além disso, olhando para o triângulo , por exemplo, podemos encontrar :
E utilizando , podemos obter :
Tendo esses valores, o próximo passo é determinar as reações de apoio em a partir do equilíbrio de momentos em torno do ponto
Passo 2
Para descobrirmos o módulo, direção e sentido das forças atuando nas barras, precisamos sempre partir de um ponto/nó que tenha uma força com módulo, direção e sentido conhecidos.
Show! A partir disso, podemos analisar os nós da treliça separadamente, que devem estar em equilíbrio para que a treliça também esteja. Começando pelo nó :
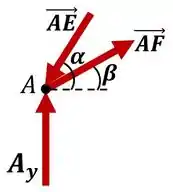
Agora podemos fazer o equilíbrio de forças nas direções e :
Sempre que uma força apontar para o nó ela é de compressão , ou seja, tende a comprimir a barra. Se apontar para fora, ela é de tração e tende a alongar a barra.
Passo 3
Show, feito isso, vamos repetir esse procedimento para alguns outros nós até descobrirmos as forças em todas as barras. Analisando agora o nó .
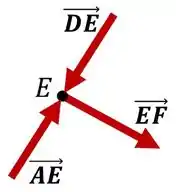
Observe que todo o carregamento que “chega” em pela barra , é transferido totalmente para a barra . Como não há nenhuma outra força externa aplicada neste nó, podemos concluir, pela condição de equilíbrio, que:
Com isso, em temos a seguinte configuração:
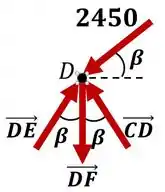
E novamente utilizando as equações de equilíbrio de força, temos:
Passo 4
Tá quase acabando hein?! Não desiste não!! Hahaha
Bora analisar o nó agora!
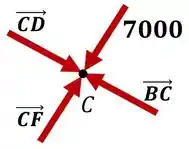
Neste caso, como as forças são perpendiculares entre si, obtemos diretamente pela condição de equilíbrio do nó que:
Restou apenas a força na barra para ser determinada, vamos analisar então o nó (lembrando que ):
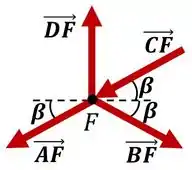
E, finalmente, fazendo o equilíbrio de forças na direção :
Sendo assim, a barra que suporta a maior força é a barra e o esforço é de tração.
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 