Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 46
A treliça mostrada é composta por 45 ∘ triângulos retângulos. Os membros cruzados nos dois painéis centrais são tirantes delgados, incapazes de suportar compressão. Retenha as duas hastes que estão sob tensão e calcule as magnitudes de suas tensões. Encontre também a força no membro MN
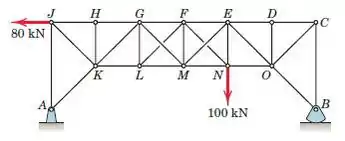
Passo 1
Primeiro temos que calcular o momento de todas as forças externas; podemos obter a força de reação no ponto B.
Passo 2
Em seguida, cortamos DE, EO e NO.
Observando o momento em torno de O de todas as forças externas (agora os membros cortados atuam como forças externas), podemos obter DE.
Passo 3
Olhando no momento sobre B de todas as forças externas, podemos obter EO.
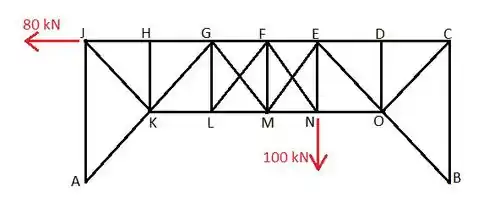
Passo 4
A seguir, vamos ver toda a treliça e como ela se move sob forças externas. A força em J está puxando sua parte superior para a direita e a força em N está puxando sua parte inferior. Truss está sendo esticado na direção dos membros GM e FN, então devem haver tensões e os membros FL e EM são compressões e podemos excluí-los da foto. Apenas as forças verticais que atuam em E são componentes verticais de EO e EN, então:
Agora, olhando para o ponto N, podemos ver que os membros EN e FN estão combatendo a força externa.
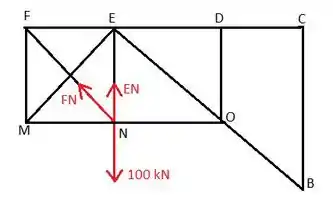
Passo 5
Em seguida, apenas as forças verticais em F são FM e a componente vertical de FN e apenas as forças verticais em M são FM e a componente vertical de GM. A partir disso, sabemos que GM e FN devem ser iguais.
Finalmente, olhando para o ponto N e as forças horizontais agindo sobre ele, podemos obter o memeber MN.
