Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 50
(a) Calcule o momento da força de em relação ao ponto para a condição . Determine também o valor de para o qual o momento em relação a é (b) zero e (c) máximo.
Passo 1
Em um problema como esse é importante usar o Teorema de Varignon, ou seja, lembrar que podemos calcular o momento de uma força em relação a um ponto olhando para os momentos das componentes em relação ao mesmo ponto.
No caso a força tem uma componente na direção vertical:
E outra na direção horizontal:
E o sinal negativo aparece porque essa componente aponta para a esquerda no eixo horizontal.
Passo 2
(a) Agora podemos calcular os momentos de cada uma dessas forças em relação ao ponto , e então somá-los.
Começamos pelo momento de :
Porque é a distância entre a linha de ação da força e o ponto .
Pela mesma lógica:
E agora podemos somar tudo para encontrar o momento total:
No caso em que e :
Passo 3
(b) Agora vamos usar a mesma equação para determinar o para o qual o momento é igual a zero:
Dividindo tudo por :
E esse é o caso em que a linha de ação da força é paralela à distância até o ponto .
E a outra possibilidade acontece quando o vetor está na mesma direção e sentido oposto, para encontrá-la é só somar :
Passo 4
(c) E o caso máximo acontece quando a linha de ação da força é perpendicular à distância até o ponto . Aqui podemos deixar o teorema de Varignon de lado:
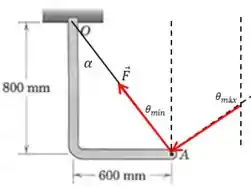
Nosso objetivo é calcular o , que é o ângulo formado pela força com a distância até o ponto no caso em que essas duas direções são perpendiculares.
Pela imagem podemos escrever a seguinte relação:
Mas o ângulo pode ser encontrado da seguinte forma:
E então:
E a outra possibilidade acontece quando o vetor está na mesma direção e sentido oposto, para encontrá-la é só somar :
Resposta
(a)
(b) ou
(c) ou