Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 131
Um caminhão-baú, com um cavalo mecânico de 2.000 kg um baú 8.000 kg, viaja em uma estrada nivelada a 90 km/h. Os freios da carreta do baú traseiro falham e o sistema antiderrapagem do cavalo-mecânico fornece a maior força possível para evitar que as rodas deslizem. Sabendo que o coeficiente de atrito estático é 0,65, determine (a) o menor tempo necessário para o caminhão parar, (b) a força no engate durante esse tempo.
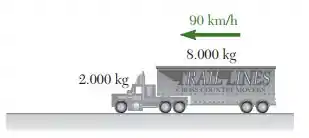
Passo 1
Vamos então resolver mais esse exercício de dinâmica. Para determinar o menor tempo para o caminhão parar e a força no engate vamos usar mais uma vez o princípio de impulso e quantidade de movimento linear. Vamos observar primeiro como esse princípio funciona através do diagrama de corpo livre:
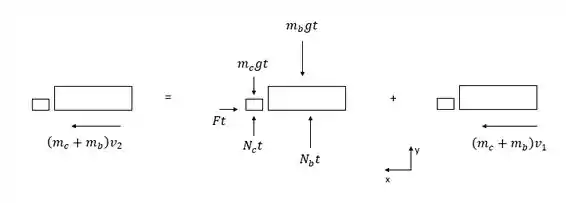
Pelo diagrama, vemos que a quantidade de movimento linear do conjunto em um segundo momento é dado pela combinação do impulso provocado pelo sistema antiderrapagem do cavalo mecânico e pela quantidade de movimento inicial. Como os freios do baú falharam, a força de frenagem será igual a força de atrito estático entre as rodas do cavalo-mecânico e o solo. Assim, somando na direção x temos:
Passo 2
A velocidade inicial do caminhão, em m/s, é:
Assim temos que o tempo necessário para o conjunto parar será:
O tempo necessário para o caminhão parar será de 19,60 s.
Passo 3
A força no engate, que é aplicada sobre o baú (onde o engate é fixado), pode ser obtida utilizando o mesmo princípio dos passos anteriores. Pelo diagrama de corpo livre somente para o baú temos:
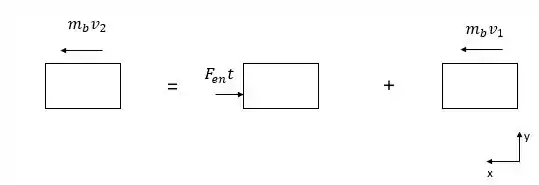
Assim, somando os vetores na direção x temos:
A força no engate será de 10,20 kN.
Resposta
- 19,60 s
- 10,20 kN