Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 1
Um bloco de 2,5 kg inicia a uma velocidade de 3m/s em um aclive liso de 45°, determinar o tempo que o bloco se moverá aclive acima até parar.
Passo 1
Podemos fazer um diagrama de corpo livre e identificar as forças que estarão agindo no bloco, e, sabendo que o aclive é liso, logo não teremos atrito, então:
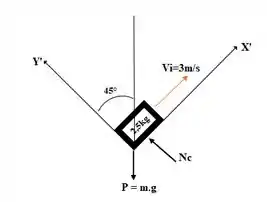
Adotando o plano X’-Y’ para facilitar nossos cálculos, pelo DCL podemos ver que estarão agindo apenas as componentes da normal Nc e da força peso P.
Passo 2
Sabendo que o bloco se moverá na direção positiva de X’, temos que:
Como , e aplicando os valores de m = 2,5 kg e g = 9,81m/s², temos que:
Resposta
O bloco subirá o aclive liso de 45° por 0,4329 segundos até para e ser igual a 0.
Exercícios de Livros Relacionados
19. Um bloco de 15Kg move-se inicialmente por uma superfície horizontal lisa, com uma velocidade escalar v 1 = 1,8 m s para esquerda. Se sobre ele age uma forca F, que varia do modo mostrado, determin
20. Determine a velocidade de cada bloco 2 segundos depois de serem liberados do repouso. Despreze a massa das polias e da corda.
Uma linha de n esferas similares, cada uma com massa m , estão colocadas próximas uma a outra, como mostrado. Se a esfera 1 tem uma velocidade v 1 , determine a velocidade da n - 1 -ésima. O coeficien
Um bloco A de 10k g é liberado do repouso 2m acima da placa P de 5k g , que pode deslizar livremente sobre as guias verticais lisas B C e D E . Determine a velocidade do bloco e da placa logo após o i
O caminhão de 5M g e o carro de 2M g estão viajando nas velocidades mostradas imediatamente antes de colidirem. Após a colisão o carro move-se com uma velocidade de 15k m / h para a direita em relação