Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 133
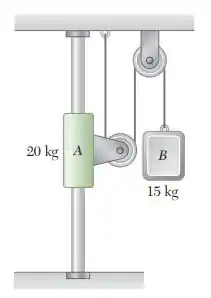
O sistema mostrado na figura é liberado do repouso. Determine o tempo necessário para a velocidade de A atingir 1 m/s. Despreze o atrito e a massa das roldanas.
Passo 1
Esse parece ser um exercício interessante, porque envolve os conhecimentos dos capítulos anteriores sobre cinemática. Aqui temos um sistema de roldanas, em que a corda tem comprimento constante, mas podemos dividir em partes para analisar a velocidade dos blocos:
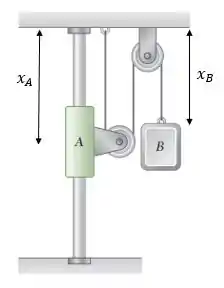
Como o comprimento da corda é constante, temos que:
Derivando em relação ao tempo, podemos encontrar uma relação entre as duas velocidades:
Isso significa que as velocidades possuem sentidos opostos, e que o bloco B está descendo e o colar A está subindo. Vamos considerar que se a velocidade aponta para baixo, o sinal é positivo.
Passo 2
Para analisar o princípio do impulso, vamos considerar como positivo o sentido de baixo para cima. Considerando como a força de tração das cordas, temos para o colar A e o bloco B:
Multiplicando a segunda equação por -2 e somando com a primeira:
Passo 3
A velocidade final do colar A é 1,0 m/s. Como aponta para cima, . Assim, . Substituindo os valores para massa e velocidade, temos que o tempo necessário será de:
Resposta
t = 0,815 s