Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 23
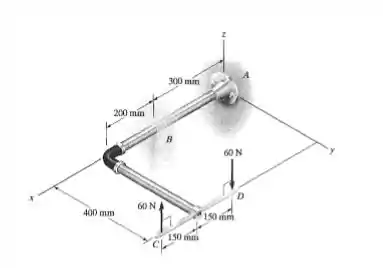
O cano tem massa de . Se ele estiver fixado à parede em , determine as cargas internas resultantes que agem na seção transversal em . Despreze o peso da chave .
Passo 1
Oláaaa, querido! Tá bem?
Então, ele quer saber as cargas internas que atuam na seção que passa por . Para fazer esse tipo de questão, a primeira coisa é cortar nossa peça na seção que ele pediu, escolher um dos pedaços e fazer o diagrama de corpo livre da situação nova.
A gente escolhe o pedaço que não tem apoio. Percebe que o pedaço tem o apoio, a gente não sabe as reações nesse apoio, então falta uma informação desse pedaço. Já o pedaço não tem apoio, logo vai ser melhor usar ele.
Então vamos cortar nossa estrutura em olhar só para o pedaço que tem os pontos . Assim:
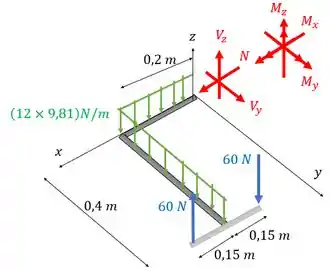
Aí a gente posiciona na seção as nossas cargas que queremos calcular na seção . Como estamos no 3D, teremos 6 cargas: 3 momentos (as setinhas duplas) e 3 forças.
Percebe que a gente tem uma carga distribuída que representa o peso do cano. Como ele deu em a gente multiplica o valor dela por para ter algo em .
A ideia é a gente usar as equações de equilíbrio para achar o valor dessas 6 cargas. Bora lá!
Passo 2
Como podemos ver, temos cargas distribuídas e para transformá-las em cargas concentradas vamos multiplicar a carga pela distância em que ela é aplicada, sendo o ponto de aplicação da carga concentrada na metade da distância. Fica assim
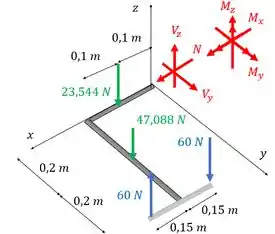
Agora é aplicar as equações de equilíbrio. Olhando para o equilíbrio de forças em :
Para o eixo :
E para :
Passo 3
Agora vamos usar as equações de equilíbrio para os momentos. A gente vai considerar como positivo os sentidos dos momento representados no DCL. Vamos repetir nosso DCl aqui para facilitar nossas continhas:
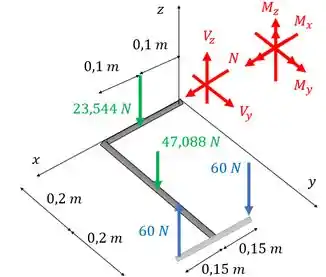
Olhando para o equilíbrio de momentos em relação a :
Percebe que a gente não considerou o par de forças de aqui porque eles formam um binário que apenas vai gerar momento em relação a . O momento que uma força de faz em relação ao eixo cancela o momento que a outra força de faz.
E falando em momento em relação ao eixo :
O gabarito do livro achou esse valor, mas positivo. Mas fica tranquilo, é mais uma questão do referencial que ele usou para positivo.
E por fim, o momento em relação a :