Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 114
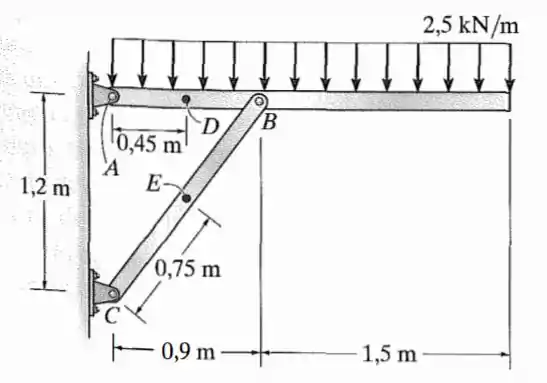
Determine as cargas internas resultantes que agem nas seções transversais que passam pelos pontos e da estrutura.
Passo 1
Para encontrarmos as forças internas que agem nos pontos destacados pela questão devemos calcular, primeiramente, as reações dos suportes. Vamos começar olhando a barra que contém o segmento AC:
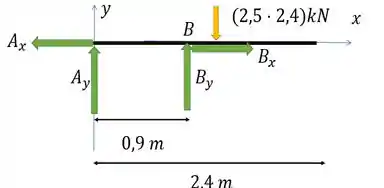
Tomando o sentido anti-horário como positivo vamos ter
Da trigonometria
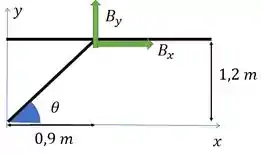
Igualando, teremos:
E por fim:
Passo 2
Agora vamos olhar cada barra, para acharmos os esforços internos nas seções que ele pediu.
- Seção : vamos olhar só para o lado a esquerda de (lembrando de considerar a carga distribuída):
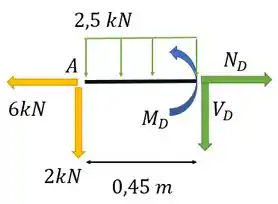
Repara que eu coloquei todos os esforços a determinar já com a orientação positiva da convenção. Aí a gente já os acha com o sinal certinho. Aí é usar as equações de equilíbrio novamente:
Tomando o sentido anti-horário como positivo vamos ter
Passo 3
- Seção : Vamos achar o módulo de :
Aí para o segmento temos
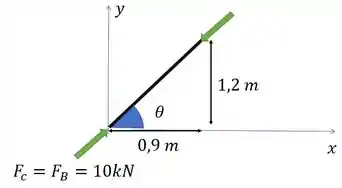
Repara que vai ter um sentido contrário nessa barra, por causa do principio ação e reação em relação a barra de cima. Olhando para essa figura, vemos que:
Negativo, porque o esforço está entrando na seção.
Resposta
Segmento
Segmento