A viga é suportada por um pino em e também por um cabo . Um cabo separado é usado para manter a estrutura na posição vertical. Se pesar e o peso da coluna for , determine as cargas internas resultantes que agem nas seções transversais localizadas nos pontos e . Despreze a espessura da viga e da coluna nos cálculos.

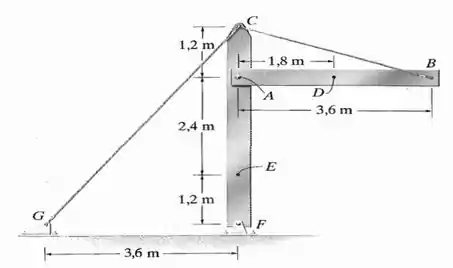
Para achar os esforços em , precisamos calcular as reações de apoio para o membro .

Vamos decompor assim:

Esse é o cosseno do ângulo que faz com a horizontal.

E esse é o seno.

Adotando o sentido anti-horário como positivo para o momento teremos

Para as forças na vertical (adotando para baixo como positivo) teremos

Agora, se liga nisso aqui: a gente acha pela decomposição:

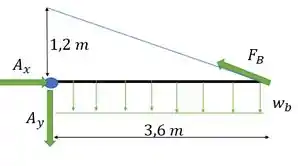
Pronto, calculamos tudo para o segmento e agora vamos trabalhar com a coluna trabalhando de forma análoga ao anterior, de tal forma que obtemos

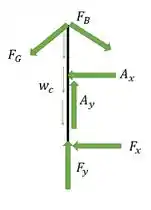
Com essas forças calculadas, a gente pode olhar para , e cortar essa barra em e olhar só para o lado direito. Na seção, colocamos as componentes dos esforços internos e achamos eles pelas equações de equilíbrio, assim:

Adotando, para o momento, o sentido anti-horário como positivo vamos ter

Ânimo que já vamos terminar essa questão.

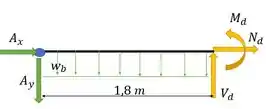
Bom, já encontramos as forças internas para , resta-nos, agora, voltarmos nossa atenção para o segmento para obter as reações internas em , utilizaremos os mesmos procedimentos de análise anterior. Vamos olhar para a parte de baixo da barra:

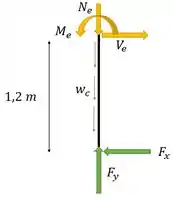
Pronto, acabamos mais um probleminha puxado, tudo certo por aí?