Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 30

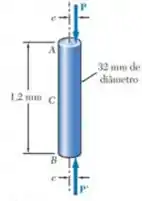
Uma carga axial P é aplicada à haste de aço AB com 32 mm de diâmetro conforme mostrada. Para P = 37   k N   e e = 1,2   m m ,   determine (a) a deflexão do ponto médio da haste em C, (b) a tensão máxima na haste. Utilize E = 200 G P a

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a deflexão do ponto médio da haste em C e a tensão máxima na haste.

Vamos começar calculando a inércia e a força P vem comigo :D

I = π 4 d 2 4 = π 4 32 2 4 = 51,47 × 10 3 m m 4 = 51,47 × 10 9 m 4

L e = L = 1,2 m

P c r = π 2 E I L e 2 = π 2 200 × 10 9 51,47 × 10 - 9 1,2 2 = 70,556 × 10 3 N

P P c r = 37 × 10 3 70,556 × 10 3 = 0,52440

Passo 2

Agora vem comigo para o cálculo da deflexão :D

y m a x = e sec ⁡ π 2 P P c r - 1 = 1,3817 e = 1,3817 1,2

y m a x = 1,658

Passo 3

Para determinarmos a tensão máxima temos que começar calculando o momento máximo e a área primeiramente :D

M m a x = P e + y m a x = 37 , × 10 3 1,2 + 1,658 10 - 3 = 105,75 N ∙ m

A = π 4 d 2 = π 4 32 2 = 804,25 m m 2 = 804,25 × 10 6 m 2 ,     c = 16 × 10 - 3 m

Agora sim a tensão

σ m a x = P A + M c I = 37 × 10 3 804,25 × 10 - 6 + 105,75 16 × 10 - 3 51,47 × 10 - 9 = 78,9 × 10 6 P a

σ m a x = 78,9   M P a

Resposta

  1. 1,658
  2. 78,9   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra é feita de liga de alumínio 2014-T6. Determine sua espessura b, se a largura for 5b. Considere que ela está acoplada por pinos nas extremidades.
Usando as equações AISC, selecione no Apêndice B a coluna de aço estrutural de menor peso que tenha 4,2 m de comprimento e suporte uma carga axial de 200 kN. As extremidades estão presas por pinos. Ad
Usando as equações de AISC, selecione no apêndice B a coluna de menor peso que tenha 3,6m de comprimento e suporte uma carga axial de 200 kN. As extremidades estão engastadas. Considere σ y = 350 M P
O tubo tem 6 mm de espessura, é feito de liga de alumínio 2014-T6 e está engastado na base e preso por pinos no topo. Determine a maior carga axial que ele pode suportar.
Determine o maior comprimento de uma seção W250 x 18 de aço estrutural A-36, se ela tiver engastada e sujeita a uma carga axial de 140 kN. Use as equações AISC.