Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 51
A carga axial P é aplicada em um ponto localizado sobre o eixo , a uma distância do eixo geométrico do perfil laminado de aço da coluna . Quando , nela é observado que a deflexão horizontal no topo da coluna é de . Usando , determinar: (a) a excentricidade e da carga; (b) a máxima tensão na coluna.
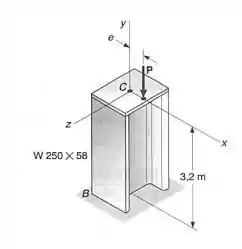
Passo 1
E ai gurizada tudo certo? O enunciado pede que a gente determine: (a) a excentricidade e da carga; (b) a máxima tensão na coluna, vamos começar trazendo os dados do elemento :D
Para
Passo 2
Vamos começar determinando a força P pedida no item (a), partiu?
Como no enunciado foi dado que a deflexão horizontal no topo da coluna é de , temos então:
Passo 3
Show de bola! Agora para o item (b) precisamos determinar a tensão máxima na coluna, para isso:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
3. Uma coluna de aço A - 36 tem comprimento de 4,0m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
A coluna ABC tem uma seção transversal retangular uniforme com b = 12 m med = 22 m m . A coluna é contraventada no plano xz em seu ponto médio C e suporta uma força centrada P de intensidade de 3,8 kN
A coluna AB suporta uma força centrada P de intensidade de 66 kN. Os cabos BC e BD estão esticados e impedem o movimento do ponto B no plano xz. Usando a fórmula de Euler e um coeficiente de segurança
x z em seu ponto médio C. (a) Determine a relação b/d para a qual o coeficiente de segurança é o mesmo em relação à flambagem nos planos xz e yz. (b) Usando a relação encontrada na parte a, projete a