Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 26
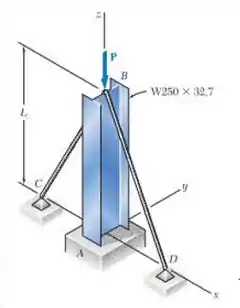
A coluna AB suporta uma força centrada P de intensidade de 66 kN. Os cabos BC e BD estão esticados e impedem o movimento do ponto B no plano xz. Usando a fórmula de Euler e um coeficiente de segurança de 2,2, e desprezando a tração nos cabos determine o comprimento L máximo admissível. Use
Passo 1
Partiu determinar o comprimento L máximo admissível. Temos os seguintes dados:
A força P é dada por:
Passo 2
No plano xz temos:
Passo 3
No plano yz temos:
O menor valor de L governa, então:
Resposta
O menor valor de L governa, então:
Exercícios de Livros Relacionados
10.13 Determine o raio da escora redonda de modo que as escoras redonda e quadrada tenham seção transversal de mesma área e calcule a carga crítica de cada escora. Utilize E = 200 GPa.
Determine (a) a carga crítica para a escora quadrada, (b) o raio da escora redonda para o qual ambas as escoras têm a mesma carga crítica. (c) Expresse a área da seção transversal da escora quadrada c
A haste de aço BC é conectada à barra rígida AB e ao apoio fixo em C. Sabendo que G = 11,2 × 1 0 6p s i , determine o diâmetro da haste BC para o qual a carga crítica P c r do sistema é de 80 lb.
10.7 A barra rígida AD está conectada a duas molas de constante k e está em equilíbrio na posição indicada. Sabendo que as cargas iguais e opostas P e P’ permanecem horizontais, determine a intensidad
10.22 Uma barra de alumínio quadrada de 25,4mm de lado é mantida na posição mostrada na figura por um apoio articulado em A e por conjuntos de roletes em B e C que impedem a rotação da barra no plano