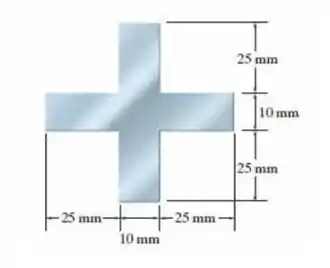
3. Uma coluna de aço tem comprimento de e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.

Vamos determinar os momentos de inércia em relação aos eixos e , respectivamente e .

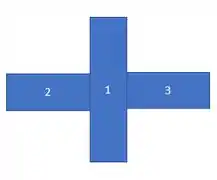
Calculemos o momento de inércia em relação ao eixo

Logo, substituindo os valores numéricos pertinentes, chegamos à:

Não vamos fazer a bobagem de perder tempo calculando o momento de inércia em relação ao eixo , né? A nossa coluna de aço tem a mesma simetria em relação ao eixo e . Logo o momento de inércia vai ser igual à .

Na fórmulinha a gente usa o menor momento de inércia. Isso porque usamos o momento do eixo em tornodo qual nossa coluna tende a flambar. Como nesse caso eles são iguais. Usamos qualquer um.

Agora que já conhecemos nossos momentos de inércia, vamos usar a fórmula de Euler, para a carga crítica da flambagem:

Vamos então, substituir os valores numéricos de cada variável:

Só falta a gente verificar se nossa carga é satisfatória, calculando o valor da tensão crítica também, né ?! Porque essa carga não pode causar uma tensão que ultrapasse a tensão de escoamento do material, beleza?

Sabemos que ela é dada pela seguinte fórmula (a divisão da carga crítica pela área da seção transversal):

Esse valor é muito menor do que a tensão admissível para o aço . Então, tudo ok com nossa coluna!