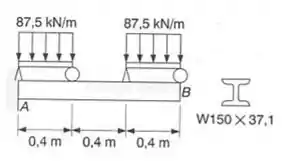
As cargas distribuídas mostradas são suportadas por pequenas vigas, que descansam sobre a viga em balanço AB. Usando , determinar a declividade e a deflexão no ponto da viga em balanço.
- Declividade em B;
Passo 1
Como a carga está agindo nas barras de cima, mas queremos a deformação na viga AB, precisamos determinar as reações da barra superior e passar elas para a barra AB.
Assim as reações de apoio são dadas por:
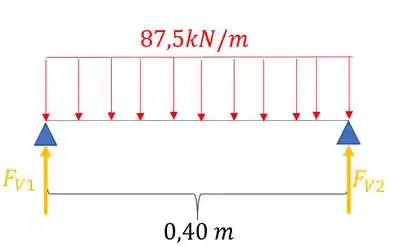
Passo 2
Agora que temos a reação, podemos transferir as cargas para a barra de baixo, e basta determinarmos a deformação na barra de baixo em cada ponto, porque ai vamos ter quando o ponto em B caiu, assim, temos que a nossa viga é dada por:

Precisamos dividir as cargas na nossa viga, e assim, teremos que:
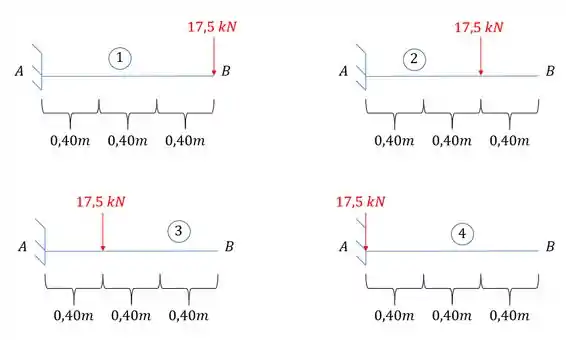
Perceba que vou focar na declividade do ponto B, que é o nosso objetivo.
- declividade na viga 1
- Deformação na viga 2
- Deformação na viga 3
- Deformação na viga 4
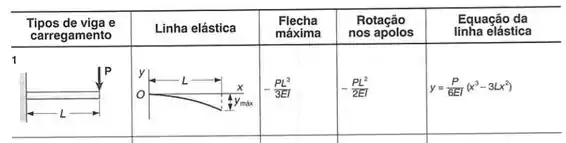
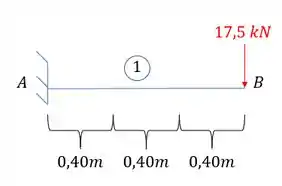
Como a carga está na ponta da nossa viga, temos que a deformação do nosso ponto B vai ser dado por:
A inercia e modulo de elasticidade da nossa viga são dadas por:
Assim a deformação em B é dada por:
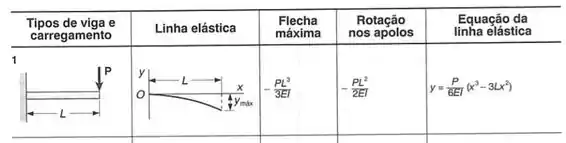
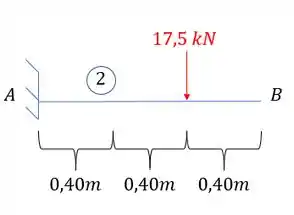
Considerando a posição da carga, podemos considerar ela como sendo o final da nossa viga engastada, assim, vamos determinar a deformação e o ângulo no ponto que ela está aplicada e depois transferimos ele para o nosso ponto B, assim, temos que:
Sabemos que:
Assim a deformação calculada é dada por:
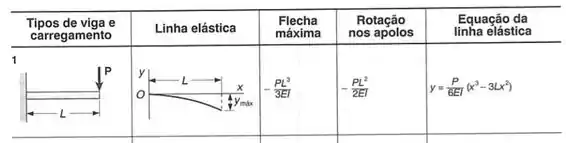
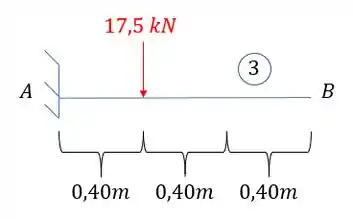
Considerando a posição da carga, podemos considerar ela como sendo o final da nossa viga engastada, assim, vamos determinar a deformação e o ângulo no ponto que ela está aplicada e depois transferimos ele para o nosso ponto B, assim, temos que:
Sabemos que:
Assim a deformação calculada é dada por:
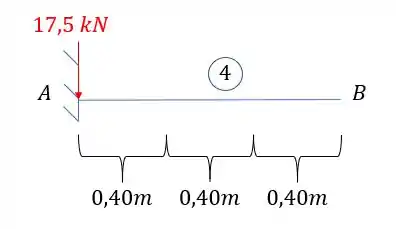
Como o ponto A é um engaste, temos que:
Assim a deformação do ponto B é a soma de todas as outras, assim ela vai ser dada por: