Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 112
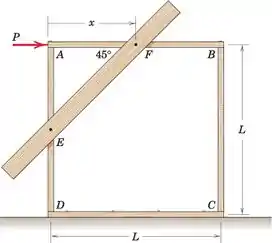
O carpinteiro constrói a moldura quadrada ABCD e, em seguida, amarra-a com o membro EF, conforme mostrado, a fim de evitar o empilhamento (distorção em uma forma rômbica) sob a força aplicada P. Determine a tensão T na cinta como uma função de x. Considere todas as conexões como juntas de pino. O membro DC está firmemente preso ao chão.
Passo 1
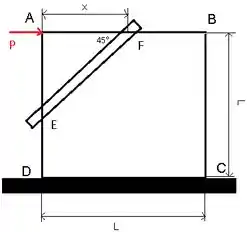
O carpinteiro constrói a moldura quadrada ABCD e, em seguida, amarra-a com o membro EF, conforme mostrado, a fim de evitar tracionamento (distorção na forma rômbica) sob a força aplicada P. Determine a tensão T na cinta como uma função de x. Considere todas as conexões como juntas de pino. O membro DC está firmemente preso ao chão.
Passo 2
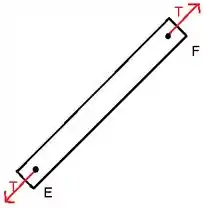
O membro EF é dois membros da força e está sob tensão T (veja a imagem abaixo).
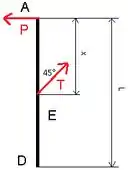
Se isolarmos o membro AD e observarmos o momento em torno de D, podemos encontrar a tensão T como uma função de x. Observe que o ângulo entre AB e EF é constante de 45º, portanto, alterando x, não alteramos esse ângulo.
Passo 3
Além disso, a força externa P está agindo no membro AB à direita, mas como A é uma junta de pino, ela está agindo em AD à esquerda.
