Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 110
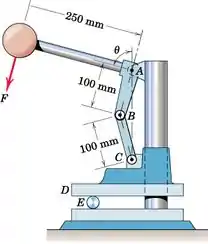
A mandíbula superior D da prensa de alternância desliza com resistência ao atrito desprezível ao longo da coluna vertical fixa. Calcule a força compressiva R exercida sobre o cilindro E e a força suportada pelo pino em A se uma força F = 200 N for aplicada ao cabo em um ângulo
Passo 1
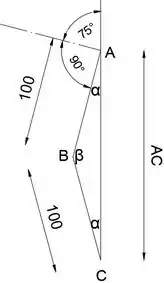
Primeiro, resolveremos o triângulo ABC para determinar o ângulo que os membros AB e AC formam com o eixo y e a distância entre os pontos A e C
Uma vez que o triângulo ABC é isósceles, os ângulos nos pontos A e C são iguais
Vamos assumir que o membro AB e a alça formam um ângulo reto, portanto, o ângulo é
Angulo beta é
Passo 2
Como sabemos os lados AB e BC e o ângulo b, usando a regra do cosseno, determinaremos o comprimento do lado AC
Passo 3
Agora vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da parte AB
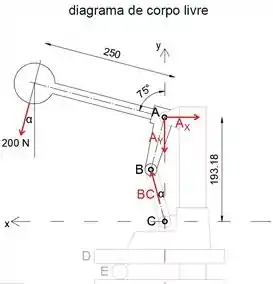
Ao igualar a soma dos momentos sobre o ponto A a zero, eliminaremos as forças de reação em A, para que possamos determinar a força de reação BC
Passo 4
Equacionando a soma das forças na direção x e y a zero, determinaremos as forças de reação em A
Passo 5
Usando o teorema de Pitágoras, podemos determinar a magnitude da força de reação em A
A seguir, vamos desmembrar o dispositivo e desenhar o diagrama de corpo livre da mandíbula superior D
Observe que há força de reação normal N da barra vertical atuando no diagrama de corpo livre
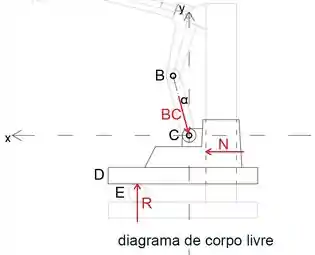
Passo 6
Equacionando a soma das forças na direção y a zero, determinaremos a força de reação R